基于F-K和Radon变换的多次波衰减方法

引用本文

张亚伟, 严加永, 刘振东, 张永谦, 徐峣. 基于F-K和Radon变换的多次波衰减方法[J].中国地质调查, 2015,2(3): 22-27.
ZHANG Ya-wei, YAN Jia-yong, LIU Zhen-dong, ZHANG Yong-qian, XU Yao. Multiples Attenuation Approach by F-K and Radon Transform[J].Geological Survey of China, 2015,2(3): 22-27.
复制到剪切板

Permissions

基于F-K和Radon变换的多次波衰减方法

张亚伟^1,², 严加永², 刘振东², 张永谦², 徐峣²

1. 中国电建集团贵阳勘测设计研究院有限公司, 贵州贵阳 550081

2. 中国地质科学院矿产资源研究所,国土资源部成矿作用与资源评价重点实验室, 北京 100037

严加永(1977—),博士,副研究员,从事矿产资源深部探测。 Email:yanjy@163.com。

作者简介: 张亚伟(1987—),硕士研究生,地球探测与信息技术专业。 Email:yaawee.zhang@gmail.com。

收稿日期: 2015-01-03

基金资助: 中国地质调查“破碎蚀变岩型金矿深部找矿勘查技术集成(编号:12120114053301)”、中央级公益性科研院所基本科研业务费(编号:k1217)和国家自然科学基金(编号:41104061)项目联合资助

摘要

多次波干扰是地震勘探中最重要的问题之一,其衰减技术也是地震数据处理的难题之一。本文主要介绍了多次波的形成、分类及其特征,并在ProMax系统上对合成地震记录的多次波进行了压制:首先采用合适的速度对时-空域的地震记录进行NMO校正;然后,分别用F-K变换和Radon变换方法将其变换到F-K域和Radon域,对多次波所占据的主要区域进行充零衰减;最后,通过对应的反变换将其变换到时-空域,从而达到多次波衰减的目的。通过在ProMax系统中的应用表明:不同方法对多次波的衰减效果各有优劣,组合滤波方法能达到更好的效果。

关键词: 多次波; NMO校正; F-K变换; Radon变换; 地震勘探

中图分类号:P631.4 文献标志码:A 文章编号:2095-8706(2015)03-0022-06

Multiples Attenuation Approach by F-K and Radon Transform

ZHANG Ya-wei^1,², YAN Jia-yong², LIU Zhen-dong², ZHANG Yong-qian², XU Yao²

1. Guiyang Engineering Corporation Limited of Power China,Guiyang,Guizhou 550081, China

2. Institute of Mineral Resources, Chinese Academy of Geological Sciences, MLR Key Laboratory of Metallogeny and Mineral Assessment, Beijing 100037, China

Abstract

Multiples is one of common noises in seismic exploration, the techniques of multiples attenuation is a serious problem in seismic data processing. This paper introduced the formations, classifications, characteristics of multiples, and the multiples attenuation in synthetic seismic data in ProMax system. Firstly, NMO correction with the appropriate speed for CDP gathers in t-x domain; Secondly, used F-K transform and Radon transform respectively to convert it to different domains, then attenuated the area where multiples was in new domains; Finally, transformed it to t-x domian through the corresponding inverse transforms to achieve the purposes of the multiples attenuation. By the applying of multiples attenuation in ProMax system, it suggests that different methods of multiples attenuation have advantages and disadvantages, and multiples attenuation in combination with different methods will achieve better results.

Keyword: multiples attenuation; NMO correction; F-K transform; Radon transform; seismic exploration

Show Figures

随着地震勘探的深入, 特别是海洋、油气和深部勘探技术的发展, 多次波压制问题越来越引起人们的重视。多次波是地震勘探中比较常见的干扰波之一, 其压制技术也一直是地震资料处理的难题。多次波的出现和存在, 使目的层反射波的振幅、频率和相位发生畸变, 影响了地震成像的真实性和可靠性, 因此如何有效地压制多次波成为地震资料处理的一个关键的问题。

目前生产中压制多次波的方法主要有滤波法和波动方程预测相减法。滤波法基于地震信号的运动学特征, 利用多次波与一次波特征和性质上的差异进行多次波压制, 如周期性、时差差异等, 比较典型的方法有:预测反褶积、正常时差变换叠加、F-K变换、τ -p变换、Radon变换和聚束滤波等^{[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]}。波动方程预测相减法基于弹性波动理论, 兼顾地震信号运动学特征, 通过从地震数据中将预测出的多次波模型进行自适应相减进行压制, 主要方法有:波动方程外推法、反馈环法和反散射级数法等^{[14, 15, 16, 17]}。基于波动方程预测的多次波压制方法可处理复杂地下介质的地震资料, 但计算成本较高。基于滤波的多次波压制方法计算效率较高, 但其成功应用仅局限于一次波和多次波有明显时差差别的地震数据, 对来自速度逆转等复杂介质数据则较难获得满意的压制效果^[18]。

压制多次波的方法有很多种, 由于不同方法其原理和针对性也有所不同, 并且各有优劣, 一般在实际应用中某种单一方法压制多次波很难取得理想效果, 也没有任何单一的方法适用于所有类型的多次波衰减。

1 多次波分类及其特征

1.1 多次波的形成

地震勘探是利用地下介质的波阻抗差异, 通过观测和分析大地对人工激发地震波的响应, 推断地下岩层的性质和形态的一种地球物理勘探方法。在海洋地震勘探中, 海水与地层的波阻抗差异很大, 因此它们之间形成了一个强反射界面; 而对于地下介质, 强反射界面可能是由速度和岩性的不同、不整合或沉积间断所引起的差异性界面, 当反射波向上传播遇到某个具有较大波阻抗差的界面时, 反射波有可能从这个界面反射, 向下传播, 当遇到反射界面时, 再次发生反射返回地(海)面, 因此从理论上来说, 只要存在波阻抗的差异, 就会形成多次波。

1.2 多次波特征

(1)在单炮记录上, 多次波表现为相同位置与有效波不同的曲率特征, 其反射时差比一次波大, 并与一次波呈等时差间隔多次出现, 同相轴振幅以规则的方式增加或者衰减。

(2)在时间剖面上, 多次波的倾角随多次波的阶数增大而增大, 并且多次波的阶数越高, 其携带的构造痕迹越多, 产生多次波地层的构造能够引起多次波聚焦和发散效应, 如在向斜底部和背斜两翼边缘聚焦。

(3)在速度谱上, 与产生多次波地层速度相同或相近的位置有强能量显示, 同时在时间上表现为周期性特征。

2 理论基础

2.1 F-K变换

在地震资料处理中, F-K变换是压制多次波最常用的方法之一。F-K变换其实就是两个变量(时间t和炮检距x)的二维傅立叶变换, 它将信号分解成不同频率的指数函数(即正弦和余弦), 把地震数据d(x, t)由时-空域变换到频率-波数域, 即:

D(f, k)=ʃ ʃ d(x, t)e²^j^{π (}^ft+kx⁾dxdt(1)

d(x, t)=ʃ ʃ D(f, k)e²^j^{π (}^ft+kx⁾dfdk(2)

式中:f为频率; k为波数; x是空间变量; t是地震数据的双程旅行时; d(x, t)表示地震数据; D(f, k)表示F-K变换域数据。通常把F-K变换的双重傅立叶变换看作是地震数据的平面波分解, 可以解释为F-K域中的一个点代表了时-空域中的一个简谐平面波。

2.2 Radon变换

在地震资料的处理中, Radon变换定义为:

u(τ , p)= $\begin{matrix} ʃ_{- \infty}^{+ \infty} \end{matrix}$ d(t=τ +pφ (x), x)dx(3)

式中:τ 是时间截距; p表征曲线的曲率特征; x是空间变量; t是地震数据的双程旅行时; d(t, x)表示地震数据; u(τ , p)为Radon变换域数据; φ (x)描述Radon变换积分曲线的曲率。如果定义积分变量中, 当t=τ +px, 就是线性Radon变换; 当t=τ +px², 就是抛物线Radon变换; 当t= $\begin{matrix} \sqrt{τ^{2} + p x^{2}} \end{matrix}$ , 就是双曲线Radon变换。

3 多次波压制在ProMax上的实现

3.1 合成地震记录及NMO校正

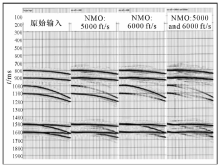
首先, 利用表1中不同参数的合成60道的CDP道集, 道间距为50 ft, 偏移距为零偏移距, 再利用不同的NMO校正速度(5 000 ft/s、6 000 ft/s、10 000 ft/s和12 000 ft/s)进行NMO校正。如图1所示:由于多次波比一次波的反射时差要大, 当采用接近多次波的速度5 000 ft/s或6 000 ft/s进行NMO校正时, 一次波同相轴明显校正过量呈上翘状, 多次波同相轴被拉平; 当采用接近一次波速度10 000 ft/s或12 000 ft/s进行NMO校正时, 一次波同相轴轻微校正过量被拉平, 多次波同相轴几乎没有变化。

表1 合成地震记录参数 Table 1 Parameter of synthetic seismic data

	Figure Option View Download New Window
	图1 不同速度的NMO校正Fig.1 NMO with different velocity

3.2 F-K变换压制多次波

3.2.1 F-K域分析

对合成地震记录进行NMO校正后, 将其变换到F-K域, 并对其分析是非常重要的一个环节。为了便于分析, 从模型中提取一条一次波同相轴(t=800 ms, v=10 000 ft/s)和一条多次波同相轴(t=1 000 ms, v=5 000 ft/s), 利用不同的速度(5 000 ft/s、5 500 ft/s和10 000 ft/s)进行NMO校正, 然后将其变换到F-K域, 如图2所示:当采用多次波速度5 000 ft/s进行MNO校正, 一次波几乎完全位于负波数区域; 当采用比多次波速度略大的速度5 500 ft/s进行MNO校正, 一次波大多数位于负波数区域, 小部分位于正波数区域; 当采用一次波速度10 000 ft/s进行NMO校正, 一次波几乎完全位于正波数区域。因此, 为了获得较好的滤波效果, 采用接近多次波速度进行NMO校正。

	Figure Option View Download New Window
	图2 F-K域分析Fig.2 Analysis of F-K domain

F-K滤波方法的基本思路为:首先, 利用多次波速度在时-空域中对合成记录进行NMO校正后, 一次波同相轴校正过量向上翘, 而多次波校正不足向下弯曲, 这时一次波存在着负时差, 而多次波存在着正时差; 然后, 进行二维傅氏变换, 在F-K域它们分别位于零波数轴的两侧, 一次波位于负波数区域, 多次波位于正波数区域, 对正波数区域进行充零进行多次波的切除; 最后通过二维傅氏反变换回时空域, 从而达到了压制多次波的目的。

3.2.2 F-K变换滤波

采用不同的速度进行NMO校正后的F-K变换切除滤波的结果如图3所示:当NMO校正速度为5 000 ft/s时, F-K滤波基本只对速度为5 000 ft/s的两个多次波起作用; 当NMO校正速度为6 000 ft/s时, F-K滤波基本只对速度为6 000 ft/s的两个多次波起作用。因此, 先利用速度为5 000 ft/s进行NMO校正后滤波, 再利用速度为6 000 ft/s进行NMO校正后滤波, 其滤波效果对v=5 000 ft/s的两个多次波和对v=6 000 ft/s的两个多次波都起作用, 叠加了两种最佳NMO校正速度滤波的效果。

	Figure Option View Download New Window
	图3 F-K变换压制多次波Fig.3 Multiples attenuation in F-K transform

利用F-K变换压制多次波的过程中, 其滤波效果好坏的关键是NMO校正的速度的选取。当一次波和多次波存在着较小的速度差异时, 一次波和多次波不能完全分离到负波数和正波数区域, 所以多次波压制效果不是很理想。F-K变换压制多次波容易出现假频和失真现象, 数据重建能力和保幅能力弱, 由于是线性分区, 近偏移距处的一次波同相轴也遭到了破坏。

3.3 Radon变换压制多次波

3.3.1 Radon域分析

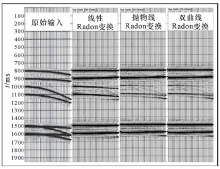
利用Radon变换进行多次波压制前应该对其在Radon域进行分析, 如图4所示:当采用线性Radon变换到Radon域时, 多次波被拉长, 占据的区域与一次波相重叠; 当选用抛物线和双曲线Radon变换到Radon域时, 多次波和一次波分别占据不同的区域, 几乎没有相互重叠的区域, 因此采用抛物线和双曲线Radon变换可以得到较好的多次波压制效果。另外, 采用20~60 ms的顶部切除参数可以使切除线远离一次波的位置(图4中红线), 使一次波的振幅受到的影响较小, 达到较好的切除效果。

	Figure Option View Download New Window
	图4 Radon 域分析Fig.4 Analysis of Radon domain

3.3.2 Radon变换滤波

Radon变换法是对地震资料沿给定的路径进行积分, 其基本思路为:首先, 利用表1的参数合成与F-K变换中相同的模型; 其次, 利用多次波和一次波的速度差异, 在采用一次波速度(v=10 000 ft/s)对合成地震记录进行NMO校正后, 将地震数据通过不同的Radon变换将其变换到新域, 多次波和一次波能在新域变换成点状并占据不同的区域, 再将该域的多次波进行切除; 最后通过Radon反变换得到时-空域内不含多次波的数据。根据不同的求和路径, Radon变换又分为线性Radon变换、抛物线Radon变换和双曲线Radon变换。

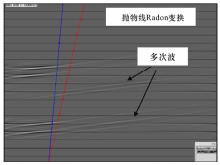
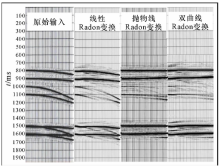
不同的Radon变换压制多次波效果如图5所示:线性Radon变换滤波效果比较差, 抛物线和双曲线Radon变换滤波的效果相对较好, 双曲线变换对于深层的多次波有更好的结果。由于近偏移距处一次波和多次波的时差较小, 因此在近偏移距附近的滤波效果不太理想。

	Figure Option View Download New Window
	图5 Radon变换压制多次波Fig.5 Multiples attenuation in Radon transform

3.4 F-K域和Radon域组合压制多次波

组合压制多次波思路为:分别先后用v=5 000 ft/s和v=6 000 ft/s进行NMO校正后采用F-K变换滤波, 再用F-K滤波后的地震记录作为Radon变换滤波的输入数据, 将其变换到Radon域, 如图6所示:可以看到位于切除线右侧的多次波在Radon域明显减弱, 然后在Radon域进行切除, 得到滤波后结果如图7所示。组合滤波对多次波的压制效果比单一的F-K滤波和拉冬滤波效果都要好, 对近偏移距处的多次波也有了进一步的削弱, 但是还有一定残留。

	Figure Option View Download New Window
	图6 F-K变换滤波后Radon域分析Fig.6 Analysis of Radon domain after filtering in F-K transform

	Figure Option View Download New Window
	图7 组合压制多次波Fig.7 Multiples attenuation in combination

4 结论

本文通过对多次波的压制方法在ProMAX上的实现, 通过理论分析和输入模型的建立, 以及对各影响参数的试验。分析了F-K变换和Radon变换两种方法对多次波的压制效果, 以及它们的优缺点, 得到了如下结论:

(1) F-K变换的优点是处理效率高, 操作过程简单。缺点是必须知道哪一层产生的多次波, 并且F-K滤波是线性分区, 在近偏移距附近的一次波同相轴遭到了一定的破坏。

(2) Radon变换的优点是不需要知道是哪一层产生的多次波, 它在所有偏移距等量地衰减多次波, 缺点是对近偏移距处的多次波不能进行较好的压制。

(3)采用F-K域和Radon域组合压制多次波可以取得比单一压制更好的效果。

(4)由于多次波形成机制复杂, 目前没有任何一种单一的方法可以对多次波进行完全的压制, 不同的多次波压制方法各有优劣, 如果能取长补短, 利用几种不同的方法对多次波进行压制, 将会取得比较理想的结果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Weglein A B. Multiple at tenuation: an overview of recent advances and the road ahead[J]. The Leading Edge, 1999, 18(1): 40-44. [本文引用:1]
[2]	渥·伊尔马滋. 地震资料分析——地震资料处理、反演和解释[M]. 北京: 石油工业出版社, 2006: 122-216. [本文引用:1]
[3]	Egbai J C, Atakpo E, Aigbogun C O. Predictive deconvolution in seismic data procesing in Atala prospect of rivers State, Nigeria[J]. Advances in Applied Science Research, 2012, 3(1): 520-529. [本文引用:1]
[4]	Ryu J V. Decomposition(DECOM) approach applied to wavefield analysis with seismic reflection records[J]. Geophysics, 1982, 47(6): 869-883. [本文引用:1]
[5]	吴律, 武克奋, 孙力. τ-p 变换方法及其在地震资料处理中的应用[J]. 石油物探, 1986, 1: 4. [本文引用:1]
[6]	Taner M T. Long-period sea-floor multiples and their suppression[J]. Geophysical Prospecting, 1980, 28(1): 30-48. [本文引用:1]
[7]	Hampson D. Inverse velocity stacking for multiple elimination[M]. SEG Annual Meeting. Society of Exploration Geophysicists, 1986. [本文引用:1]
[8]	Sachi M D, Ulrych T J. High resolution velocity gathers and of set space reconstruction[J]. Geophysics, 1995, 60: 1169-1177. [本文引用:1]
[9]	刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15. [本文引用:1]
[10]	郭全仕, 张卫华, 黄华昌, 等. 高精度拉冬变换方法及应用[J]. 石油地球物理勘探, 2005, 40(6): 622-627. [本文引用:1]
[11]	胡天跃, 王润秋. 地震资料处理中的聚束滤波方法[J]. 地球物理学报, 2000, 43(1): 105-115. [本文引用:1]
[12]	胡天跃, 王润秋. 聚束滤波法消除海上地震资料的多次波[J]. 石油地球物理勘探, 2002, 37(1): 18-23. [本文引用:1]
[13]	洪菲, 胡天跃, 张文坡, 等. 用优化聚束滤波方法消除低信噪比地震资料中的多次波[J]. 地球物理学报, 2005, 47(6): 1106-1110. [本文引用:1]
[14]	牛滨华, 沈操, 黄新武, 等. 波动方程压制多次波的技术方法[J]. 地学前缘, 2002, 9(2): 511-517. [本文引用:1]
[15]	张军华, 周振晓, 张雷, 等. 基于反馈环的多次波压制方法研究[J]. 地震学报, 2010, 32(1): 60-68. [本文引用:1]
[16]	金德刚, 常旭, 刘伊克. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 2008, 51(4): 1209-1217. [本文引用:1]
[17]	李翔, 胡天跃. 逆散射级数法去除自由表面多次波[J]. 地球物理学报, 2009, 52(6): 1633-1640. [本文引用:1]
[18]	石颖, 王维红. 基于波动方程预测和双曲 Radon 变换联合压制表面多次波[J]. 地球物理学报, 2012, 55(9): 3115-3125. [本文引用:1]

1999

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2006

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2012

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

1982

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

1986

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

1980

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

1986

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

1995

0.0

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2004

0.0

刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15.

Radon transformation is employed commonly in seismic data processing, especially in the events identification and estimation. The least square inversion scheme is the most ordinary method to implement the Radon transform, both for slant stack and for general Radon transform. Although many and many study have been made, there are a lot of works needed doing in enhancing the transform revolution and the computation efficiency. In this paper ,Parabolic Radon Transform （PRT） and Hyperbolic Radon Transform（HRT） have been studied by least square inversion .In the implementation of the methods, sparse constraint preconditions conjugate gradient method has been applied for enhancing the resolution. Compared to the damped least square method, the sparse constraint preconditions conjugate gradient method has advantages. This is proved by a synthetic model. On base of the difference of residual move-out between the primary and the multiple reflections, the multiple could be suppressed by Radon transform. The principals and the schemes of the method are presented in the paper with a real example. It shows that the sparse constraint precondition conjugate gradient method is proper for enhancing the Radon transform resolution , the efficiency and the accuracy are very well, and by the algorithm multiple can be suppressed better.

Institute of Geology &Geophysics,Chinese Academy of Sciences, Beijing 100029,China

Radon变换方法在地震资料处理中广泛采用,在地震同相轴识别和估计方面具有良好效果.无论是倾斜叠加,还是广义Radon变换方法,一般采用最小二乘反演方法实现.目前,在提高反演算法的效率和分辨率方面仍值得研究.本文从倾斜叠加的定义出发,阐明Radon变换分辨率问题的来源和解决办法.采用最小二乘反演方法研究高分辨率抛物线Radon变换和双曲Radon变换时,给出稀疏约束预条件共轭梯度法求解的高分辨率Radon变换的实现方法,同阻尼最小二乘方法相比,分辨率和精度明显提高,文中给出了模型算例.根据有效波和多次波NMO后剩余时差不同,采用高分辨率抛物线和双曲Radon变换可以压制多次波,分别给出了方法原理,最后给出应用实例.研究表明,稀疏约束预条件共轭梯度法可以有效实现高分辨率Radon变换;数值算例表明,算法计算效率和精度较高,可以更好地实现多次波压制.

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2005

0.0

郭全仕, 张卫华, 黄华昌, 等. 高精度拉冬变换方法及应用[J]. 石油地球物理勘探, 2005, 40(6): 622-627.

Random transform has been widely used in seismic exploration, for example, suppression of multiple,separation of P- and S-waves,seismic migration and inversion etc.The paper briefly introduced linear, hyperbolic and parabolic Random transform methods as well as sparse-constrained inversion and adaptive wave separation algorithm further developed on that basis; analyzed their advantages and disadvantages in the respects of scanning velocity, recognizing ability and wavefield restoration by synthetic data.It is shown a satisfactory effect by using these methods to suppress multiple in surface seismic exploration and tube wave in cross-hole seismic exploration.

拉冬变换在地震勘探领域有广泛的应用,如压制多次波、纵横波分离、地震偏移及反演等。本文简要介绍线性、抛物线和双曲线拉冬变换方法,以及在此基础上进一步发展起来的稀疏约束反演和自适应波场分离算法; 并通过合成数据模型比较了各种方法在扫描速度、分辨能力和波场恢复方面的优势和不足;将这些方法应用到地面地震的多次波压制和井间地震的管波消除,取得了令人满意的效果。

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2000

0.0

胡天跃, 王润秋. 地震资料处理中的聚束滤波方法[J]. 地球物理学报, 2000, 43(1): 105-115.

Minimum variance unbiased （MVU） beamforming is a type ofmultichannel filtering which extracts coherent signals without distortion, whilstminimizing residual noise power. Adaptive beamforming estimates signal and noisecharacteristics as part of the extraction process. This paper gives the fundamentalprinciple of beamforming including signal and noise model, design criteria and theobtained beamformer. The adaptive beamformer used here is designed from models ofprimary and multiple reflection signals having parametrically specified moveout,amplitude and phase variation with offset （MVO, AVO and PVO）. However, PVO isnot usually jushfied in practice. The resulting analysis provides data for input intoAVO and PVO schemes for obtaining lithological information. Synthetic data examplesillustrate details of implementation of parametric adaphve MVU beamforming and theresponse characterishcs of the resultaflt design. Real data examples show thatdata-adaptive beamforming is more flexible and more effective in attenuating multiplesin prestack common mid point seismic data than Radon transform methods. Incommon with other prestack multichannel processes, the advantages of beamformingare shown to best effect in data with a good signal-to-noise ratio.

聚束滤波方法的基本原理，包括信号与噪音模型、设计准则和所获得的聚束滤波器．本文所用的自适应聚束滤波器是根据具有参数化的动校正量、振幅及相位随偏移距变化（ＭＶＯ、ＡＶＯ及ＰＶＯ）的一次反射和多次反射信号模型而设计的．但在实际应用中ＰＶＯ通常不能得到证实．结果分析能为进一步的从ＡＶＯ及ＰＶＯ获取岩石类型信息的专题研究提供资料．人工合成资料的例子给出了参数化的自适应聚束滤波的实施细节和所设计滤波器的响应特性．实际资料的例子表明数据自适应聚束滤波在叠前共中点道集地震多次波消除上比Ｒａｄｏｎ变换方法更灵活、有效．类似于其它叠前处理过程，自适应聚束滤波的优越性在信噪比较高的资料上体现得最为明显．

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2002

0.0

胡天跃, 王润秋. 聚束滤波法消除海上地震资料的多次波[J]. 石油地球物理勘探, 2002, 37(1): 18-23.

This paper briefly introduced the principle of using beam-forming filtering method to attenuate multiple from seismic data and the results of processing synthetic data.The procedure and results of using beam-forming filtering method to attenuate multiples in two data sets from deep sea area of South China Sea are discussed in details.In order to attenuate the multipies generated by coral riff which are strong and large in scope,we implement the beam-forming filtering method several times to attenuate the multiples in different ranges and obtain the optical results of relatively high resolution with a relatively small computational effort.The processing results show that beam-forming filtering method can attenuate some relatively very strong multiples generated by coral riff and enhance the relatively weak primaries.The example of deep water data from southeast Yin Basin that there are strong sea-bottom multiple shows that beam-forming filtering method can attenuate multiples very well at traces on both near and far offsets,and the results are better than that by using the conventional 2-D multipies attenuation method.

本文简单介绍了用聚束滤波方法消除地震资料中的多次波的基本原理及合成资料处理结果;详细描述了用聚束滤波方法消除两套南海深海地区地震资料中多次波的实施步骤与效果。对于珊瑚礁产生的大范围强烈多次波,采用多次使用聚束滤波方法分别消除不同范围的多次波,取得了较高分辨率和较小计算量的优化效果。处理结果表明,聚束滤波方法可以消除相对较强的多次波,并增强较弱的一次波。对莺东南盆地一块海底多次波相当严重的深水地震资料的处理结果表明,聚束滤波方法对于消除远道和近道多次波的效果都相当好,并且优于常规的二维滤波方法对多次波的压制效果。

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2005

0.0

洪菲, 胡天跃, 张文坡, 等. 用优化聚束滤波方法消除低信噪比地震资料中的多次波[J]. 地球物理学报, 2005, 47(6): 1106-1110.

We present an optimal beamforming method and its application to attenuating multiple for low signaltonoise (S/N) ratio seismic data，which is better than some popular techniques like fk and Radon transformation．The key point of the method is updating the constraint in the optimal beamformer design by using adaptive beamformer with the quiescent weighted vector．The example of real data processing example shows that this optimal beamformer method has improved the minimum variance unbiased beamformer significantly in attenuating multiples for low folding and/or low S/N ratio data at small extra cost．

针对常规方法如fk，Radon变换不能很好解决的消除低信噪比地震勘探资料的多次波问题，本文提出了优化聚束滤波方法，采用具有静态权的自适应聚束滤波器，并调整聚束滤波器设计的约束准则，去除低信噪比复杂实际资料中的多次波．实际资料处理结果表明，优化聚束滤波方法改善了最小方差无偏聚束滤波方法不能较好地处理低覆盖低信噪资料处理的局限性，在实际处理中计算量增加不大．

... -p变换、Radon变换和聚束滤波等^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} ...

2002

0.0

牛滨华, 沈操, 黄新武, 等. 波动方程压制多次波的技术方法[J]. 地学前缘, 2002, 9(2): 511-517.

多次波问题是海洋地震勘探中最突出的问题之一,如何有效地压制多次波是解决问题的关键.多次波数据处理的压制方法和技术分为运动学的滤波方法和动力学的波动方程方法两大类.波动方程方法由于几乎不需要先验信息和具有较好的压制效果,已经成为多次波压制方法和技术发展的主要趋势.文章首先对波动方程方法进行了较全面的综述;然后,对波动方程方法中的反馈迭代反演方法做了深入的讨论;最后,通过理论模型的正反演计算,验证了运用波动方程反馈迭代反演法不需要知道震源函数、地下岩层结构和岩性等先验信息.此方法适用于压制多种类型的多次波,具有优异的振幅保真性等独特的优点.

... 波动方程预测相减法基于弹性波动理论,兼顾地震信号运动学特征,通过从地震数据中将预测出的多次波模型进行自适应相减进行压制,主要方法有:波动方程外推法、反馈环法和反散射级数法等^{[14,15,16,17]} ...

2010

0.0

2008

0.0

金德刚, 常旭, 刘伊克. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 2008, 51(4): 1209-1217.

There are two wave-equation methods to attenuate internal multiples. One is CFP (common focus point) continuation method which is proposed by Berkhout and Verschuur(1998). The other is ISS(inverse scattering series) method which is proposed by Weglein etc. (1997). ISS method is independent of velocity. But the computing cost is very high. Firstly, we deduce a new algorithm based on the 1D ISS predicting formula given by Weglein et al. The new algorithm is about 12 times more efficient than the old algorithm in theory. Actually testing result shows that it is faster, nearly 80 times. In addition, internal multiple prediction in temporal spatial domain has more advantages than in pseudo-depth wavenumber domain. We deduce 1.5D ISS predicting formulation in temporal spatial domain from the 2D ISS formulation given by Weglein et al. The new formulation has some important merits, for example, high computing efficiency, little predicting noise, easiness to suit to geometry and independence of seismic wavelet. It is difficult to use old ISS algorithm to predict internal multiples of field data because of high computing cost. Based on the modified algorithm, we discuss the strategy of internal multiple prediction to make it usable on field data.

Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China

波动方程预测层间多次波有两类算法.一是由Berkhout和Verschuur（1998）提出的基于CFP（共聚焦点）延拓的算法，另一是由Weglein（1997）等人提出的基于逆散射级数法的算法.ISS（逆散射级数）算法具有不依赖速度模型的优点，但是其计算成本很高.本文改进了Weglein提出的1-D预测公式，提高了计算效率.从理论方面，改进算法的计算速度提高了大约12倍.实际结果表明其计算速度更快，提高近80倍左右，主要原因在于后者的空间复杂度小.此外，由于时间-空间域比伪深度-波数域的层间多次波预测有更多的优点，本文推导了1.5-D时间-空间域ISS层间多次波预测算法，该算法有计算速度快、预测噪音小、适应观测系统能力强和不依赖地震子波等优点.在实际应用中，计算成本高是ISS预测层间多次波算法的主要障碍.因此，本文还讨论了预测层间多次波的策略.结合本文提出的改进算法和应用策略，能够在实际地震资料处理中较好地应用ISS预测层间多次波.

2009

0.0

李翔, 胡天跃. 逆散射级数法去除自由表面多次波[J]. 地球物理学报, 2009, 52(6): 1633-1640.

Multiple removal is a key process in seismic data processing, the effect of multiple elimination directly affects the final imaging. In this paper, inverse scattering series method is based on wave equation and Born series, multiples are predicted and removed by constructing a subseries corresponding to surface-related multiples. This method does not need any subsurface information and is suitable for different kinds of complex structures. However, source wavelet and near offset traces information will be needed for applying this technique. Energy minimizing method and band-limited parabolic Radon transform is employed to meet the above two conditions. The examples of a synthetic data study and a marine data show that the free-surface multiple can be well attenuated in both prestack gathers and seismic section by implementation with inverse scattering series method.

压制多次波是地震资料处理过程中的重要环节之一，多次波去除的效果直接影响到最后成像的质量．本文研究的逆散射级数法以波动方程和Born级数为基础，构造一个与自由表面多次波相关的子序列来预测并消除多次波，该方法不需要知道地下的速度结构信息，适用于各种复杂的地下情况．在逆散射级数法的实现过程中，地震子波和近道波场是必不可少的信息，本文采用能量最低法则和带限抛物Radon变换法来弥补原始地震资料中所缺失的这些信息．合成资料和实际地震资料的处理结果表明，逆散射级数法能够在去除自由表面多次波的同时保留有效波的信息，对于地下复杂结构的情况同样有效．

2012

0.0

石颖, 王维红. 基于波动方程预测和双曲 Radon 变换联合压制表面多次波[J]. 地球物理学报, 2012, 55(9): 3115-3125.

Surface-related multiple suppression method based on wave equation prediction can handle seismic data from complex subsurface, but the computational cost is high. For filter-based multiple suppression method, its computation efficiency is high, but it is only limited to the seismic data which has enough moveout difference between the primary and multiple. It is difficult to obtain satisfactory suppression effect for the seismic data from complex media, such as velocity reversal. The proposed algorithm combines wave equation prediction with filtering method effectively, surface-related multiple is predicted approximately by the collaborative parallel acceleration calculation from GPU(graphic processing unit) and CPU, followed by comparing and analyzing original data and predicted multiple in the hyperbolic Radon domain. We design an effective adaptive Butterworth-type filter to select the multiple energy from original data in Radon domain. After inverse Radon transform, suppression result can be obtained by subtracting multiple from original data with multiple. The theoretical single-shot data, complex SMAART model and field data are tested by the proposed algorithm. The results demonstrate that the multiple suppression method in the article can breakthrough the limitations of wave equation based method and hyperbolic Radon transform effectively, which can suppress surface-related multiples from complex subsurface efficiently and accurately.

基于波动方程预测的表面多次波压制方法可处理复杂地下介质的地震资料,但计算成本较高.基于滤波的多次波压制方法计算效率较高,但其成功应用仅局限于一次波和多次波有明显时差差别的地震数据,对来自速度逆转等复杂介质数据则较难获得满意的压制效果.本文将波动方程预测的反馈迭代法和滤波法有效结合,采用GPU(图形处理器)和CPU协同并行加速计算粗略预测表面多次波,随后在双曲Radon域比较分析原始数据和预测的多次波,设计合理有效的Butterworth型自适应滤波器,滤出原始数据Radon域中的多次波能量,进行Radon反变换后,在时空域将多次波从原始数据中减去,得多次波压制结果.文中对理论模拟的单炮数据、复杂的SMAART模型以及实际地震数据进行了计算,结果表明,结合基于波动方程预测和双曲Radon变换的方法有效突破了两种方法各自的局限性,可高效高精度地压制复杂地下介质的表面多次波.

... 基于滤波的多次波压制方法计算效率较高,但其成功应用仅局限于一次波和多次波有明显时差差别的地震数据,对来自速度逆转等复杂介质数据则较难获得满意的压制效果^[18] ...