北京市门头沟区某公路岩质边坡稳定性分级研究

引用本文

郭松峰, 祁生文, 李星星, 邹宇, 廖海军, 张世殊. 北京市门头沟区某公路岩质边坡稳定性分级研究[J].中国地质调查, 2016,3(3): 55-61.
GUO Songfeng, QI Shengwen, LI Xingxing, ZOU Yu, LIAO Haijun, ZHANG Shishu. Stability classification of rock slopes along a highway in Mentougou, Beijing[J].Geological Survey of China, 2016,3(3): 55-61.
复制到剪切板

Permissions

《中国地质调查》编辑部所有

北京市门头沟区某公路岩质边坡稳定性分级研究

郭松峰¹, 祁生文¹, 李星星¹, 邹宇¹, 廖海军², 张世殊³

1.中国科学院地质与地球物理研究所,页岩气与地质工程重点实验室,北京 100029

2.北京市地质研究所,北京 100120

3.中国电建成都勘测设计研究院有限公司,成都 610072

第一作者简介: 郭松峰(1986—),男,博士后,主要从事工程地质与岩体力学方面的研究。Email: guosongfeng@mail.iggcas.ac.cn。

收稿日期: 2016-03-10

基金资助: 国家自然科学基金项目(编号: 41322020,41172272)和中国博士后基金项目(编号: 2015M581167)联合资助

摘要

北京市门头沟区某公路岩质边坡数量多,边坡物理力学性质及其影响因素复杂多变,无法获取每个边坡岩体的物理力学参数,因此,对大量边坡进行力学稳定性分析十分困难。采用层次分析和模糊综合评价方法,根据各种因素对岩质边坡稳定性影响的定性分析,确定了2级4类共9个边坡稳定性影响因子,将边坡的稳定性级别划分为4级,即稳定、基本稳定、较不稳定和不稳定; 然后,构建了隶属度矩阵和权重矩阵; 最后,对每个边坡的稳定性进行模糊综合评价。分析结果表明,在所研究的113个边坡中,不稳定边坡3个,占总边坡的3%,较不稳定边坡27个,占24%,基本稳定边坡52个,占46%,稳定边坡31个,占27%。因此认为: 当边坡数量众多、边界条件模糊、影响因素复杂时,模糊综合评判是比较合适的边坡稳定性分析方法; 应用最大隶属度原则时,需根据各种因素对边坡稳定性影响的因果关系,对最大隶属度原则的有效性进行评估,以防出现评判失效。

关键词: 公路岩质边坡; 层次分析; 模糊综合评价; 稳定性分级; 北京门头沟

中图分类号:P642 文献标志码:A 文章编号:2095-8706(2016)03-0055-07

Stability classification of rock slopes along a highway in Mentougou, Beijing

GUO Songfeng¹, QI Shengwen¹, LI Xingxing¹, ZOU Yu¹, LIAO Haijun², ZHANG Shishu³

1. Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences,Beijing 100029, China

2. Beijing Institute of Geology, Beijing 100120, China

3. Power China Chengdu Engineering Corporation Limited, Chengdu 610072, China

Abstract

The rock slopes, along a highway in Mentougou, Beijing, have characteristics as follows: huge amounts of 113, complicated influencing factors, large difficulty to gain mechanical parameters of all slopes, so it is hard to investigate the mechanical properties for large member of slopes. Analytic multilayer process and fuzzy comprehensive evaluation are used to classify the slope stability in this paper. Two-layer and four primary influencing factors including nine secondary influencing factors are chosen to evaluate the slope stability according to the influencing factors of slope stability. Firstly, the stability classification is divided into 4 grades: stable, basically stable, less unstable, and unstable. Secondly, membership matrix and weight matrix are constructed. Lastly, stability of every slope is classified by the fuzzy comprehensive evaluation. The results indicate that the number of unstable slopes is 3, 3% of all slopes; the number of less unstable slopes is 27, 24% of all slopes; the number of basically stable slopes is 52, 46% of all slopes; the number of stable slopes is 31, 27% of all slopes. If the number of slopes is huge, boundary conditions are not clear and influencing factors are complicated, fuzzy comprehensive evaluation is an eligible method. It should be noted that the validity of the maximum subordination principle should be evaluated based on the effect of every factors on slope stability in case the evaluation fails.

Keyword: highway rock slope; analytic multilayer evaluation; fuzzy comprehensive evaluation; stability classification; Mentougou,Beijing

Show Figures

0 引言

目前, 边坡稳定性分析方法主要分为定量分析方法和定性分析方法。定量分析方法主要包括极限平衡法^{[1, 2, 3, 4, 5]}、有限元强度折减法^{[6, 7, 8]}及块体理论法^[9]等。然而, 由于公路沿线边坡具有数量众多、影响因素复杂以及人类活动变化大等特点, 难以逐个获取边坡详细的物理力学参数, 因此对众多边坡稳定性的定量分析评价难以实施。因而, 建立在因果关系基础上的定性分析方法对于边坡的稳定性评价更具实用价值。模糊综合评价就是较为成熟的一种定性分析方法^{[10, 11, 12, 13]}, 这种方法应用最大隶属度原则和模糊变换原理, 综合考虑被评事物或其属性的相关因素, 对评价目标进行等级或类别划分, 适合于具有多种影响因素的边坡稳定性评判。本文通过对北京市门头沟区某公路沿线岩质边坡稳定性的定性分析评估, 介绍线路工程边坡稳定性模糊综合评价方法及其应用效果。

1 研究区概况

北京市门头沟区某公路连接G109国道与昌平区, 全长17.1 km, 是一条重要的省级公路。研究路段位于北京西山地区门头沟中部, 该区属温带大陆性季风气候, 年平均降雨量650~675 mm, 年内降水不均, 7— 8月的降雨量可达全年降雨量的60%左右。研究区与永定河成“ T” 字形交汇, 永定河为常年断流河流, 研究区内边坡受河流影响较小。

研究区出露的地层岩性包括寒武系灰岩, 侏罗系页岩、粉砂岩、玄武岩、角砾凝灰岩、粗安山岩, 第四系砂砾石以及坡积土等。岩体受地质构造影响, 小断层、节理、卸荷裂隙切割严重。研究区为山区地貌, 中间高两端低, 公路路面海拔300~500 m。边坡高6~50 m不等, 坡度几乎全部大于45° , 有些边坡近直立, 坡顶植被覆盖良好, 多数为矮草和灌木。

通过对公路沿线边坡踏勘, 确定公路沿线可能存在稳定性问题的边坡共计113个。公路经过泗家水等5个村庄, 受人为因素影响较大, 地震设防烈度为7度。

该公路地处山区, 沿线地形地质条件复杂, 修路时多采用爆破开挖边坡, 造成切坡岩体松动, 某些高陡边坡在降雨、震动等外界作用下, 极易发生崩塌失稳灾害。2010年9月30日15:40左右, 该公路K29+400 m处发生大面积塌方事件, 土石塌方总量达500 m³左右, 造成公路中断半个月之久, 严重影响交通(图1)。

	Figure Option View Download New Window
	图1 某公路K29+400 m处塌方现场Fig.1 Landslide in K29+400 m of a highway

2 评价因子及分级标准

为预防类似上述塌方事件的再度发生, 笔者对公路沿线边坡进行了逐一调查, 并对其稳定性进行了评价和分级。

2.1 评价因子集的确定

根据公路岩质边坡的特点, 确定评价指标选择的原则为: ①突出重要因子, 放弃不起作用或起作用很小的因子, 防止重要因子被次要因子削减; ②因素的独立性越大越好; ③选择宏观因素, 避开具体的物理力学性质指标。

基于上述原则, 结合国家标准、行业规范、实际场地情况及专家意见, 确定公路岩质边坡评判指标并进行分类。

影响边坡稳定性的因素主要分为易发条件(内因)和诱导因素(外因)。易发条件主要包括岩土体特征(A)和地形地貌(B)2个一级指标, 其中岩土体特征分为岩性及岩性组合(1)、坡体结构(2)和风化程度(3)3个二级指标; 地形地貌分为坡面形态(4)、边坡高度(5)、边坡坡度(6)和植被覆盖率(7)4个二级指标。诱发因素包括水文气象(C)和地震(D)2个一级指标, 前者指多年平均降雨量(8)二级指标, 后者指地震烈度(9)二级指标。具体如图2所示。

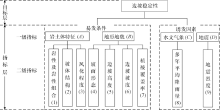	Figure Option View Download New Window
	图2 北京市门头沟区某公路边坡模糊评价层次模型Fig.2 Multilayer fuzzy evaluation model for rock slopes stability of a highway in Mentougou, Beijing

将上述分类指标编号, 可得到一级因素集为

$\begin{matrix} \begin{matrix} A = {(1), (2), (3)} \\ B = {(4), (5), (6), (7)} \\ C = {(8)} \\ D = {(9)} \end{matrix}\} \end{matrix}$ , (1)

二级因素集为

U={A, B, C, D} 。 (2)

2.2 评判集的确定

查阅相关文献, 根据研究区边坡实际情况, 将边坡稳定性划分为4个级别(表1), 由好到差依次为稳定(Ⅰ 级)、基本稳定(Ⅱ 级)、较不稳定(Ⅲ 级)和不稳定(Ⅳ 级)。单因素稳定性评价指标分级标准及基本参考条件如表1所示。评判集为

V={V_Ⅰ, V_Ⅱ, V_Ⅲ, V_Ⅳ} 。 (3)

表1 评价因子及其分级标准 Tab.1 Evaluation factors and their classification standard

3 确定隶属度

表1中的因子按数学分类法分为离散型(定性)指标和连续型(定量)指标, 分别采用公式和专家打分2种方法确定评价指标对应的隶属度。离散型指标因子有上文确定的编号(1)、(2)、(3)、(4)及(7), 采用德菲尔法, 参考相关文献, 确定其隶属度^{[11, 13]}取值情况如表2所示。

表2 离散型指标隶属度取值 Tab.2 Values of membership degree of dispersion indexes

由表2可以看出, 各指标隶属度随着稳定性级别而变, 比如若稳定性为I级, 则各指标隶属度U_Ⅰ最大, U_Ⅱ、U_Ⅲ、U_Ⅳ依次减小。对于表1中的定量指标的隶属度, 建立指标数值与隶属度之间的函数关系, 即隶属函数, 隶属度可以通过代入实际值得到。采用“ 降半梯形” 分布建立隶属函数, 其公式如下:

U_Ⅰ(x)= $\begin{matrix} \{\begin{matrix} 1 \\ \frac{b - x}{b - a} \\ 0 \end{matrix} \end{matrix}$ (x≤ a) , (3)

U_Ⅱ(x)= $\begin{matrix} \{\begin{matrix} 0 \\ - \frac{a - x}{b - a} \\ \frac{c - x}{c - b} \end{matrix} \end{matrix}$ (x< a或x> c) (4)

U_Ⅲ(x)= $\begin{matrix} \{\begin{matrix} 0 \\ - \frac{b - x}{c - b} \\ \frac{d - x}{d - c} \end{matrix} \end{matrix}$ (x< b或x> d) (5)

U_Ⅳ(x)= $\begin{matrix} \{\begin{matrix} 0 \\ - \frac{c - x}{d - c} \\ 1 \end{matrix} \end{matrix}$ (x< c) (6)

式(3)— (6)中: x为实测值; a, b, c, d为边坡稳定性分级的4个标准值。

4 确定权重系数

目前, 确定权重系数的方法有多种, 其中最常见的有层次分析法、专家打分法、德尔菲法。后2种方法受专家主观性影响大, 本文采用层次分析法确定各评价指标的权重。

层次分析法(AHP)是通过两两因素对比, 逐层比较多种关联因素, 最后确定诸因素整体关系的一种方法。该方法首先由Saaty等在20世纪70年代中期提出^{[14, 15]}, 80年代引入我国, 取得一些成果^{[11, 14, 16, 17]}。它适用于处理多因素、多目标、多层次的复杂系统工程问题, 可以达到尽可能地使主观判断与实际情况相符。

本文建立图2所示的层次模型后, 引入Saaty等的标度方法, 其含义见表3。

表3 判断矩阵标度及其含义^[17] Tab.3 Relative importance and meaning of matrix scale ^[17]

该方法根据对上一层目标的重要性大小, 对本层的因子进行两两比较, 构造相应的判断矩阵, 计算其最大特征根和对应的特征向量, 并进行判断矩阵一致性检验, 当判断矩阵的随机一致性比率C_R < 0.1时, 即认为判断矩阵具有满意的一致性, 说明权重分配是合理的。

下面以一级指标权重的确定为例, 说明这一过程。

(1)根据表3, 对4个一级指标进行两两对比, 构造判断矩阵Y。

Y= $\begin{matrix} \{\begin{matrix} 1 1 5 5 \\ 1 1 5 5 \\ 0.2 0.2 1 1 \\ 0.2 0.2 1 1 \end{matrix}\} \end{matrix}$ 。 (7)

矩阵Y中, 第i个指标与第j个指标的重要性比值为Y_ij(i为行, j为列)。比如第1个指标相对于第2、3、4个指标的重要性分别为Y₁₂= 1, Y₁₃= 5, Y₁₄= 5。

(2)计算最大特征值及特征向量.最大特征值λ _max, 归一化后的特征向量为(0.416 7, 0.416 7, 0.083 3, 0.083 3)。

(3)一致性检验。判断矩阵阶数m=4, 得到相应的一致性指标R_I=0.90, C_I、C_R分别为

$\begin{matrix} \{\begin{matrix} C_{I} = \frac{λ_{\max} - m}{m - 1} = 0 \\ C_{R} = \frac{C_{I}}{R_{I}} = 0 < 0.1 \end{matrix} \end{matrix}$ 。 (8)

判断矩阵满足一致性检验, 权重分配合理。

二级指标权重的确定方法和一级指标一样, 经过两两层次分析得到公路岩质边坡各评价指标权重(表4)。

表4 各影响因子的权重分配 Tab.4 Weight distribution for each effect factor

5 模糊综合评价

这里以边坡序号“ 101” 为例说明模糊综合评价过程。该边坡高30 m, 坡度约为60° , 为中强风化灰岩, 坡体为层状结构顺向坡, 坡体受结构面切割有大于1 m³的孤石, 较不平整, 植被覆盖情况良好(图3)。

	Figure Option View Download New Window
	图 3 边坡101图Fig.3 The No.101 slope

5.1 建立隶属度矩阵

根据上述资料, 对边坡的离散型指标按表2取值, 对于连续型指标则按式(3)— (6)计算, 可得岩土体特征因素的隶属度矩阵为

U₁= $\begin{matrix} {[\begin{matrix} 0.60 0.30 0.10 0.00 \\ 0.10 0.20 0.50 0.20 \\ 0.15 0.55 0.25 0.05 \end{matrix}]}^{T} \end{matrix}$ , (9)

地形地貌因素的隶属度矩阵为

U₂= $\begin{matrix} {[\begin{matrix} 0.00 0.10 0.65 0.25 \\ 0.00 0.00 1.00 0.00 \\ 0.00 0.60 0.40 0.00 \\ 0.50 0.30 0.15 0.05 \end{matrix}]}^{T} \end{matrix}$ , (10)

气象水文地质因素的隶属度矩阵为

U₃= $\begin{matrix} {[0.70 0.30 0.00 0.00]}^{T} \end{matrix}$ , (11)

其他因素的隶属度矩阵为

U₄= $\begin{matrix} {[0.00 0.00 0.33 0.67]}^{T} \end{matrix}$ 。 (12)

5.2 建立权重矩阵

根据确定的权重系数, 建立一级指标权重矩阵

W= $\begin{matrix} {[0.42 0.42 0.08 0.08]}^{T} \end{matrix}$ , (13)

4个一级指标下面的二级指标的权重分别为

W₁= $\begin{matrix} {[0.25 0.50 0.25]}^{T} \end{matrix}$ , (14)

W₂= $\begin{matrix} {[0.18 0.36 0.36 0.10]}^{T} \end{matrix}$ , (15)

W₃= $\begin{matrix} {[1.00]}^{T} \end{matrix}$ , (16)

W₄= $\begin{matrix} {[1.00]}^{T} \end{matrix}$ 。 (17)

5.3 计算稳定级别的隶属度

根据上述矩阵进行二级评判, 求出影响边坡稳定性的4大因数的隶属度矩阵R, 即

R={U₁W₁U₂W₂U₃W₃U₄W₄}W=

{0.18 0.24 0.44 0.14 }^T 。 (18)

式(18)表明: 该岩质边坡处于稳定状态的概率为18%; 处于基本稳定状态的概率为24%; 处于较不稳定状态的概率为44%; 处于不稳定状态的概率为14%。

5.4 确定边坡稳定级别

前人大多依据最大隶属度原则确定边坡稳定级别, 但是当算得的最大隶属度与第二大隶属度相差很小时, 显然按最大隶属度原则确定稳定级别是不合适的, 这就引出了一个最大隶属度原则的有效性问题。根据前人的研究^{[18, 19]}, 用有效性指标判断最大隶属度原则的有效性, 定义为

α = $\begin{matrix} \frac{nβ - 1}{2 γ (n - 1)} \end{matrix}$ , (19)

式中: n为归一化后的模糊综合评价判断向量R的元素个数; β 为R中的最大元素; γ 为R中的第二大元素。

如果α =+∞ , 则最大隶属度原则完全有效; 如果1≤ α < +∞ , 则最大隶属度原则非常有效; 如果0.5≤ α < 1, 则最大隶属度原则比较有效, 如果0< α < 0.5, 则最大隶属度原则低效, 如果α =0.5, 则最大隶属度原则完全失效。

若最大隶属度原则低效或失效, 则按照加权平均法、专家分析法等方法确定, 限于篇幅, 这里不对这2种方法多做介绍。

对于所给边坡, 可以算得

α = $\begin{matrix} \frac{4 \times 0.44 - 1}{2 \times 0.24 \times (4 - 1)} \end{matrix}$ =0.528> 0.5 。 (20)

故最大隶属度原则比较有效, 该边坡属于较不稳定边坡, 这与野外实际观察到的情况相符。

6 公路边坡稳定性分析结果

采用上述模糊综合评价方法对北京门头沟某公路113个岩质边坡逐个进行稳定性分析评价, 评价结果为: 稳定边坡31个, 占评价边坡总数的27%; 基本稳定边坡52个, 占46%; 较不稳定边坡27个, 占24%; 不稳定边坡3个, 占3%。该结果与野外踏勘专家判别结果基本一致。部分边坡稳定性对应的野外照片见图4, 分析评价结果见表5。

	Figure Option View Download New Window
	图4 北京市门头沟区某公路部分岩质边坡Fig.4 Some rock slopes of a highway in Mentougou, Beijing

表5 北京市门头沟区某公路部分边坡评价结果 Tab.5 Evaluation results for some rock slopes of a highway in Mentougou, Beijing

7 结论

(1)北京市门头沟某公路岩质边坡具有数量多、影响因素多、无法获取每个边坡物理参数的特点, 常规的定量分析方法在工作量、可行性等方面均不适用。

(2)模糊评判方法可以将本来模糊的、主观性很大的定性评估转变为定量评判, 适合于多变量、多影响因素的边坡稳定性评判, 思路清晰, 评判结果直观, 与层次分析法结合, 可以有效改善专家打分确定权重所带来的主观因素。

(3)将某公路岩质边坡的稳定性等级分为4级, 并对每个边坡稳定性进行模糊评价, 最后得到不稳定边坡3个, 占总边坡的3%, 较不稳定边坡27个, 占24%, 基本稳定边坡52个, 占46%, 稳定边坡31个, 占27%。

(4)在模糊综合评判中, 应对最大隶属度原则进行有效度评估。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Fellenius W. Calculation of the stability of earth dams[C]//Proceedings of the 2nd Congress on Large Dams. Washington DC, USA: Government Printing Office, 1936. [本文引用:1]
[2]	Bishop A W. The use of the slip circle in the stability analysis ofslopes[J]. Géotechnique, 1955, 5(1): 7-17. [本文引用:1]
[3]	Morgenstern N R, Price V E. The analysis of the stability of general slip surfaces[J]. Géotechnique, 1965, 15(1): 79-93. [本文引用:1]
[4]	Janbu N. Slope stability computations[R]. Soil Mechanics and Foundation Engineering Report. Trondheim, Norway: Technical University of Norway, 1968. [本文引用:1]
[5]	Sarma S K. Stability analysis of embankments and slopes[J]. Journal of the Geotechnical Engineering Division, 1979, 105(12): 1511-1524. [本文引用:1]
[6]	Griffiths D V. Finite element analyses of walls, footings and slopes[D]. Manchester: University of Manchester, 1980. [本文引用:1]
[7]	Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Géotechnique, 1999, 49(3): 387-403. [本文引用:1]
[8]	赵尚毅, 郑颖人, 邓卫东. 用有限元强度折减法进行节理岩质边坡稳定性分析[J]. 岩石力学与工程学报, 2003, 22(2): 254-260. [本文引用:1]
[9]	任青文, 余天堂. 边坡稳定的块体单元法分析[J]. 岩石力学与工程学报, 2001, 20(1): 20-24. [本文引用:1]
[10]	谢全敏, 夏元友. 岩体边坡治理决策的模糊层次分析方法研究[J]. 岩石力学与工程学报, 2003, 22(7): 1117-1120. [本文引用:1]
[11]	黄建文, 李建林, 周宜红. 基于AHP的模糊评判法在边坡稳定性评价中的应用[J]. 岩石力学与工程学报, 2007, 26(增刊): 2627-2632. [本文引用:3]
[12]	孟衡. 模糊数学在岩质边坡稳定性分析中的应用[J]. 岩土工程技术, 2008, 22(4): 178-181. [本文引用:1]
[13]	张勇慧, 李红旭, 盛谦, 等. 基于模糊综合评判的公路岩质边坡稳定性分级研究[J]. 岩土力学, 2010, 31(10): 3151-3156. [本文引用:2]
[14]	Saaty T L. A scaling method for priorities in hierarchical structures[J]. Journal of Mathematical Psychology, 1977, 15(3): 234-281. [本文引用:2]
[15]	Saaty T L, Wong M M. Projecting average family size in rural India by the analytic hierarchy process[J]. The Journal of Mathematical Sociology, 1983, 9(3): 181-209. [本文引用:1]
[16]	冯希杰, 刘玉海, 张骏. 区域稳定性评价定量化与模糊评判[J]. 西安地质学院学报, 1986, 8(4): 89-95. [本文引用:1]
[17]	聂洪峰, 祁生文, 孙进忠, 等. 重庆市区域稳定性层次分析模糊综合评价[J]. 工程地质学报, 2002, 10(4): 408-414. [本文引用:1]
[18]	陈耀辉, 孙春燕. 模糊综合评判法中的最大隶属度原则有效度[J]. 重庆师范学院学报(自然科学版), 2001, 18(1): 45-47. [本文引用:1]
[19]	陈耀辉, 孙春燕. 对最大隶属原则有效度的进一步研究[J]. 重庆师范学院学报(自然科学版), 2002, 19(1): 47-49. [本文引用:1]

1936

0.0