在能源短缺和环境污染的双重压力下, 浅层地热能作为一种清洁可再生新能源以其强大的生命力和竞争力日益受到国家和地方政府的重视^{[1, 2]}。影响浅层地热能赋存资源量的因素包括地层岩性、厚度、含水层结构、富水性、水位埋深以及补给径流条件等诸多子系统, 这类子系统数量多, 地质条件复杂, 地貌类型多样, 而且系统相互间的功能和行为不是各子系统功能和行为的简单叠加或复合, 可以称得上是“ 极其复杂的巨系统” 。

以往研究人员^{[3, 4, 5]}常使用还原论方法线性处理适宜性分区评价指标的问题, 在评价过程中, 人为的定义评价矩阵中不同地质条件的权重, 无法定量适宜性分区图。考虑到传统的定量方法对描述自然界中连绵的地层、地表及河流等自然构型方面的无力, 引入一种解决这些难题的思路和方法, 即分形理论。通过该理论, 不再将复杂的非线性问题转化为简单的线性问题来处理, 用符合浅层地热能地质地貌条件本身性质、特征的眼光来观察地质现象本身, 逐步真实、全面地刻画浅层地热能信息的性质、特征和规律。对科学评价浅层地热能赋存条件、储量估算以及分形理论的发展和延伸有较强的理论和实践意义。

本文利用回归分析法验证了浅层地热能赋存条件适宜性分区结构的分形维数, 并探讨了标度与分形维数的关系, 即证明适宜性结构分区在上述一定变化标度内具有分形结构; 通过面积-周长法和盒维数法的计算结果, 简析了面状地形地貌信息几何属性对分维值的影响。

分形^[6]原意是指不规则的物体或图形, 通过混乱现象和不规则运动揭示隐藏在它们背后的局部与整体的本质联系和运动规律。

欧式几何学的研究对象为规整的几何图像, 这类图像的长度、面积和体积的纲量分别是长度单位的1、2和3次方, 恰好与这些图形所在空间的欧式几何维数相等, 且均为整数。该维数与决定几何形状的自由度数是一致的, 因此定义自由度数作为经验维数, 但Peano曲线的出现使人们对经验维数产生了质疑, Peano曲线可定义为图中折线的极限, 一条Peano曲线可以把平面完全覆盖。该曲线处处不能微分, 被称为非规整几何图形。

同属非规整图形的还有Koch曲线、Cantor集等, 它们又被称为病态几何图形。由相似性知, 将线段、正方形和立方体的边长平均二等分, 即原先的线段、正方形和立方体可以看做是由2、4、8个个体组成的集合。2、4、8改写成21、22、23后的指数与其图形的经验维数一致。因此, 若一个图形是由全体缩小为1/a的aD个相似图形构成的, 那么D具有维数的意义, 称相似维数。D没有必要是整数, 若一个图形是由全体缩小1/a的b个相似性组成的, 相似维数为

D=ln b/ln a 。 (1)

相似维数只适用于具有严格自相似性的图形, 因此定义适用于包括随机图形在内的任意图形的维数是很必要的, 最具代表性的是1986年Mandelbrot提出的Hausdorff维数: 分形是局部和整体具有相似性的图形。该定义指出了分形的自相似性, 即分形物体具有理论上无限层次的自相似结构。

现阶段往往把取非整数值的维数统称为分形维数, 如盒子维数、面积-周长维数等, 可视为广义上的维数。由于测定维数对象不同, 就某一个分形维数的定义而言, 有些对象可能适用, 另一些则不完全适用, 因此在使用过程中往往要进行多次尝试, 找到一个对任何对象都适用的定义。

浅层地热能资源蕴藏在地下岩土体内, 其储藏、运移以及开采利用都受到区域地质、水文地质及工程地质条件等多种因素的影响, 在不同区域蕴藏于地下岩土体内的浅层地热资源规模和利用方式存在较大差异。地层岩性、厚度、含水层结构、富水性、水位埋深以及补给径流条件等是制约浅层地热能赋存分布及可利用性的主要因素。只有在浅层地热能资源开发利用方式适宜性区划的基础上, 才能进一步进行资源量计算和资源潜力评价。

分形理论产生后, 成为研究面状结构的新方法, 分维值也逐渐成为常用指标之一。目前关于浅层地热能适宜性分区结构的分形研究鲜有报道, 本文以渭南市地下水热泵适宜性分区的分形维数计算过程为例, 对该方面研究做初步探讨。

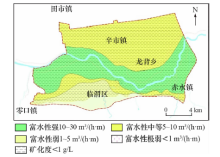
渭南市地处渭河盆地东部, 属暖温带半湿润大陆性季风气候, 四季分明。区内地势南高北低呈阶梯状降落, 为黄土台塬和渭河冲积平原, 南侧黄土台塬下为秦岭基岩山地。区内主要河流为渭河, 自西向东纵贯全区, 南岸有多条支流, 大都呈SN向平行分布。区内潜水水文地质条件良好(图1), 河漫滩、冲洪积扇含水层厚, 岩性较粗, 渗透较快, 富水性较好, 渗透系数介于13.8~98.1 m/d, 涌水量介于860~1 500 m³/d; 渭河阶地渗透系数3.7~8.48 m/d, 涌水量仅792~968 m³/d。承压水位受地形地势影响较小(图2), 河漫滩、冲洪积扇处单位涌水量介于5~15 m³/(h· m), 渗透系数介于20~50 m/d; 在渭河南部一级阶地后缘处, 单位涌水量一般< 5 m³/(h· m)。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 潜水水文地质图Fig.1 Hydrogeological map of diving water

本次浅层地热能适宜性分区评价采用综合指数法, 考虑地下水源热泵, 主要考虑含水层岩性、分布、埋深、厚度、富水性、渗透性, 地下水温、水位动态变化、水源地保护、地质灾害等指标。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 承压水水文地质图Fig.2 Hydrogeological map of confined water

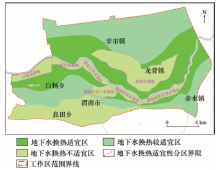
根据上述分区体系, 应用MapGIS6.7软件, 结合城区地形地貌条件、水文地质条件以及试验数据等资料, 划分出适宜性分区界限, 采用编辑子系统拓补查错和拓补重建、图面整饰等工作, 从而得到地下水地源热泵系统适宜性分区评价图。

适宜性评价分区图中根据评价指标可以分为4个区域: 浅层地热能地下水源热泵系统应用适宜区(简称适宜区)、浅层地热能地下水源热泵系统应用较适宜区(简称较适宜区)、浅层地热能地下水源热泵系统应用不适宜区(简称不适宜区)、水源地规划保护区(简称水源地)。依据规范, 水源地保护区内不允许修建地下水源热泵系统。

2.1 适宜性分区结构的分形

对浅层地热能适宜性分区结构的分形研究, 根据盒子计数法求取分形维数。盒子维数是应用最广泛的维数之一, 它的普遍应用主要是由于该维数的数学计算和经验估计相对容易。

首先定义适宜性分区结构图为一个平面集F, 构造出一个边长为r的正方形(或称盒子), 统计正方形和平面集F相交的个数N, 为了提高计算的准确率, 仅统计平面集F的覆盖面积占一半以上的正方形。通过不断调整标度r的数值, 分别统计落入盒子中的平面集F的个数N(表1)。

表1

Tab.1

表1(Tab.1)

表1 适宜性结构分区标度-频度关系 Tab.1 Relationship between scale and frequencyof suitable structure 标度/mm 适宜个数 较适宜个数 不适宜个数 水源地个数 15 141 185 140 86 20 81 112 78 46 30 33 45 34 20 40 17 22 15 7 45 13 17 12 6 60 9 11 7 3

表1 适宜性结构分区标度-频度关系 Tab.1 Relationship between scale and frequencyof suitable structure

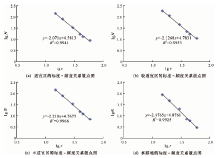
建立不同标度及该标度下落入盒子中的平面集F个数的双对数(即lg r-lg N)散点图(图3), 根据最小二乘法进行线性回归分析, 回归方程为

lg N=Dlg r+A , (2)

式中: A为待定常数; D为回归方程的斜率, 其绝对值即为分维值。

图3中的4个回归方程都通过R显著性检验, 说明浅层地热能适宜性结构分区的标度-频度关系客观存在, 即适宜性结构分区在上述的r变化标度内具有分形结构。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 适宜性结构分区标度-频度散点图Fig.3 Scatter plots of the scale and frequency of suitable structure

2.2 标度与分形维数的关系

根据分形学的数学基础可知, 自相似的分形结构具有无限嵌套结构, 在分形维数的定义中, 要求标度r趋于零时极限存在。但标度r趋于零的要求在实际测量中很难实现, 因此这个严格的数学定义并不适用于自然界中存在分形结构的研究。近年来国内外的一些学者的研究表明: 对于实际分形体而言, 测量的分形维数随着标度的变化而变化, 对同一个分形体由于选取的标度不同, 会得到不同的分维值^{[7, 8, 9, 10]}。分维值的不确定性是由于实际存在的分形物体不具有无限层次的自相似性结构, 而把适用于无限层次的分形公式用于实际的有限层次分形物体, 就可能产生分维的不确定性。因此, 测量标度r必须在一个合理的范围内, 即当r_min≤ r≤ r_max时, 测得的有限层次的分形维数是确定值D, r_min是由分形体的最小自相似结构决定的, 所以在研究实际的分形体时标度的选择不是任意的, 必须先对分形体的结构层次和存在层次进行细致的分析, 再选择标度和确定临界点。对于标度而言, 在一个合理的范围内, 有限层次的分形体的分维是恒定的; 超出此范围, 测量分维会出现不确定问题。

以2.1节中适宜区的标度-频度关系为例说明此问题。将测量尺度从15~60 mm扩展到80、90、100 mm, 绘制到双对数图上(图4)。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 测量的分维值和标度的关系Fig.4 Relationship of the fractal dimension and size

当选取的标度r满足15≤ r≤ 60时, 得到的测量数据在lg r-lg N坐标系中都落在线性区, 该直线斜率的绝对值即为分形体的测量维数; 当r≥ 80的时候, 测量数据落在非线性区, 此时的测量数据是不真实的, 得到的分维值也不是唯一的。

综上, 分形理论用于实际分形体的研究是有条件的。对标度而言, 存在一个合理的范围, 在此范围内, 分维值是恒定的; 超出此范围, 分维值就会出现不确定的问题。

将标度定义为盒子的边长r, 采用盒子法统计平面集F的覆盖面积占一半以上的正方形, 这种方法并未将图斑的周长考虑在内。下面, 首先引入常用的景观指数— — 缀块形状指数来全面地考虑图斑的周长和面积这两种因素对图斑分维数的共同影响。其次, 由于适宜性分区结构图是不规则的封闭图形, 采用周长-面积法求取其分维值, 然后与盒子计数法对比, 探讨面积和周长等属性对分维值的影响。

景观生态学中以正方形为参照几何形状的缀块形状指数S的计算公式为

S= 0.25×PA, (3)

式中: P为缀块周长; A为缀块面积。缀块形状越复杂, S值越大(表2)。

表2

Tab.2

表2(Tab.2)

表2 适宜性结构分区面积-周长关系 Tab.2 Relationship between area and perimeter of the partition of suitable structure 变量 适宜性 较适宜性 不适宜性 水源地 A 35 018.19 4 2010.02 32 981.30 19 618.19 P 2 834.37 2 265.08 2 453.29 1 689.72 S 3.79 2.76 3.38 3.02

表2 适宜性结构分区面积-周长关系 Tab.2 Relationship between area and perimeter of the partition of suitable structure

3.3 面状信息几何属性对不同分形维数的影响

整理上述3种分形维数计算方法(表3), 发现在考虑分区结构图形几何属性情况下的缀块指数和分形维数与之前的盒维数并不对应, 主要指较适宜性分区的缀块指数或分维值低于其他3项。

表3

Tab.3

表3(Tab.3)

表3 面状几何信息参数 Tab.3 Parameters of surface geometrical information 性质 适宜性 较适宜性 不适宜性 水源地 盒维数 2.07 2.13 2.22 2.48 缀块指数 3.79 2.76 3.38 3.02 面积-周长法 3.40 2.63 2.87 2.71

表3 面状几何信息参数 Tab.3 Parameters of surface geometrical information

这是由于较适宜性分区主要分布在河流南北岸的一级阶地和部分二级阶地。地层岩性上部主要为浅黄、棕黄色砂质黏土, 孔隙发育, 疏松可塑; 下部岩性主要是中粗砂和砂砾石夹砂质黏土层。该地段地下水的抽灌条件相对较好, 为采用地下水地源热泵系统的较适宜区。因此, 整个较适宜性分区呈大片区状, 边界不复杂, 贯通性好。

适宜区主要分布在河流漫滩和部分一级阶地上, 为地质条件简单强富水带地区, 地层岩性上部为粉质砂土, 疏松, 孔隙发育, 具微层理, 偶见瓦砾碎片; 下部为含砾中粗砂。地层导水性好且地下水埋深适中, 单井回灌水量与单位涌水量比值大于80%, 适宜地下水抽灌, 多年平均水位下降量小, 为采用地下水地源热泵系统的适宜区。但考虑到本区中包含数个水源地, 参照浅层地热能调查规范, 在地下水适宜性评价过程中, 水源地规划区直接列入不适宜区, 导致适宜区整体结构破碎, 边界复杂化。

地下水地源热泵不适宜区一部分分布于调查区南部河流二级阶地及黄土塬区, 富水性较差, 而且本区二级阶地顶部为一层砂质黏土, 连续性好, 层位稳定, 透水性弱; 另一部分为河流一级阶地和漫滩处的数个水源(图5)。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 渭南市浅层地热能地下水适宜性分区Fig.5 Suitability division of shallow geothermal groundwater in Weinan

盒子维数的思想与实现都较简便, 但在实际计算过程中由于一个小盒内只要包含了分形图形的一个临界点或者图形面积占小盒面积的一半以上, 该小盒就将被视为非空小盒, 因此对计算结果的精准度影响较大, 不能精准地反映分形图形的内部不均匀性^[11]。面积-周长法或缀块指数充分考虑了图形边界的曲折程度, 较符合面状信息的实际几何属性。

浅层地热能开发利用适宜性分区是资源调查评价工作的主要内容, 根据城区工程地质、水文地质等分区条件, 利用指标法确定浅层地热能适宜性分区, 评价结果科学准确, 能客观反映评价区开发利用适宜性特征。借用分形原理将已有研究中所采用的还原论方法即线性问题处理方法转换为更符合地质条件本质特征的非线性处理方法, 通过对比不同分形维数计算方法下的浅层地热能适宜性分区结构, 量化了不规则的适宜性分区图形, 探讨了面状地形地貌信息几何属性对分维值的影响, 对分形理论的实际应用和浅层地热能的开发工作都有较强的理论和实际意义。