震后坡面松散堆积体失稳水力学机理研究

引用本文

杨涛, 李明俐, 孙东, 常鸣, 杨宗佶. 震后坡面松散堆积体失稳水力学机理研究[J].中国地质调查, 2022,9(5): 40-50.
YANG Tao, LI Mingli, SUN Dong, CHANG Ming, YANG Zongji. Study on hydraulic mechanism of loose accumulation in post-earthquake slope[J].Geological Survey of China, 2022,9(5): 40-50. 复制到剪切板

doi: 10.19388/j.zgdzdc.2022.05.05

Permissions

《中国地质调查》编辑部所有

震后坡面松散堆积体失稳水力学机理研究

杨涛^1,², 李明俐³, 孙东^1,², 常鸣³, 杨宗佶⁴

1.四川省华地建设工程有限责任公司,四川成都 610081

2.四川省地质灾害防治工程技术研究中心,四川成都 610081

3.成都理工大学环境与土木工程学院,四川成都 610059

4.中国科学院水利部成都山地灾害与环境研究所,四川成都 610041

通信作者简介: 李明俐(1990—),女,讲师,主要从事泥石流灾害研究工作。Email: 784189855@qq.com。

第一作者简介: 杨涛(1990—),男,工程师,主要从事地质灾害防治方面的研究工作。Email: 1029193228@qq.com。

收稿日期: 2022-05-23 修回日期: 2022-09-30

基金资助: 国家自然科学基金“强震区降雨诱发坡面松散物源启动实验研究(编号: 42107179) ”项目资助

摘要

为研究震后强降雨条件下沟道泥石流产生的力学机制及水力学机理,以都江堰市龙池镇银洞子泥石流沟为研究对象,构建坡面松散堆积体地下水位变化水力模型,按照水力学渗流理论,分析了震后泥石流形成区坡面松散堆积体内潜水位变化的特征和规律,定量研究了动静水压力对坡体的作用特点。根据理论分析、实例验证与物理模拟试验的研究结果,获得了对坡面松散物源启动力学机理、启动临界条件及启动模式的深刻认识: ①在强降雨激发作用下,随着坡体内潜水位不断升高,水力条件不断恶化,最终导致坡面松散堆积体发生失稳破坏; ②堆积体内潜水位高度是坡面面积(S)、稳态降雨强度(I),坡体几何参数、导水系数(TD)等参数的综合函数,S、I越大,则潜水层厚度(H)越大,反之,当坡面集雨面积和稳态激发降雨强度一定时,导水系数、坡体宽度和潜水面倾角越大,则坡体内产生潜水层垂直厚度越低; ③随着坡体内静水压力(P)增加,堆积体基底抗滑力将会降低; 随着坡体内动水压力(Gd)增加,坡体下滑力将会增加; ④根据剩余下滑力的存在形式,震后坡面松散堆积体的启动模式可分为2种,即坡体整体启动的推移式失稳和分段解体启动的牵引式失稳。研究成果可为沟道泥石流的超前预警提供理论及技术支持。

关键词: 泥石流形成区; 降雨强度; 坡面松散堆积体; 潜水层厚度; 失稳启动; 力学机理

中图分类号:P642.23 文献标志码:A 文章编号:2095-8706(2022)05-0040-11

Study on hydraulic mechanism of loose accumulation in post-earthquake slope

YANG Tao^1,², LI Mingli³, SUN Dong^1,², CHANG Ming³, YANG Zongji⁴

1. Sichuan Huadi Construction Engineering Co., Ltd., Sichuan Chengdu 610081, China

2. College of Environment and Civil Engineering, Chengdu University of Technology, Sichuan Chengdu 610081, China

3. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology, Sichuan Chengdu 610059,China

4. Inst. of Mountain Hazards and Environment, Chinese Academy of Sciences, Sichuan Chengdu 610041, China

Abstract

In order to analyze the mechanical principle and hydraulic mechanism of channel debris flow under strong rainfall after earthquake, the authors take debris flow gully in Yindongzi of Longchi Town in Dujiangyan as a case study to establish the hydraulic models of underground water level change in loose accumulations. The characteristics and laws of ground water level change of loose accumulation in post-earthquake debris flow slope are analyzed according to the percolation theory in hydraulics, and the effects of hydrodynamic pressure and hydrostatic pressure on slope body are quantitatively studied. Through the combination of theoretical analysis, example verification and physical simulation test, a deep understanding of mechanical mechanism, critical condition and mode of start-up of loose source on slope was achieved. The results show that: ①Under the excitation of heavy rainfall, the hydraulic condition deteriorates continuously with the increasing diving level in the slope, which eventually leads to the stability failure of the loose accumulation body on the slope. ②The phreatic level generated by the accumulation body is a comprehensive function of slope area S, steady-state rainfall intensity I, slope geometric parameters ( θ、 W、 H、 Z) water conductivity coefficient T and other parameters. Tthe larger and I are, the higher the height of phreatic level H will be; Conversely, under the premise that the rainfall collecting area and steady-state rainfall intensity are determined, the larger T, W and θ are, the lower the phreatic level generated in the slope body will be. ③With the increasing hydrostatic pressure P in slope body, the sliding resistance of accumulation body base will be decreased; As the hydrodynamic pressure G_d inside the slope increase, the sliding force of the slope will increase. ④According to the existence form of residual sliding force, the starting mode of the loose accumulation body on the slope after earthquake can be divided into two types: the sliding mode of the whole slope starting and the traction mode of the disintegration in segments starting. The research results can provide theoretical and technical support for the advance warning of gully debris flow.In For the study of earthquake under the condition of strong rainfall channel debris flow mechanics and hydraulics mechanism, combining with the town of Dujiangyan order of the silver named debris flow gully is analyzed, the construction of slope are underground water level change under the premise of hydraulic model, with the aid of seepage theory of hydraulics, area after the earthquake were analyzed by slope loose accumulation is the characteristics and regularities of the variation of the groundwater level in the body, The effects of hydrodynamic pressure and hydrostatic pressure on slope body are quantitatively studied. Through the combination of theoretical analysis, example verification and physical simulation test,

Keyword: debris flow area; rainfall intensity; loose accumulation in slope; phreatic level thickness; destabilization starting; mechanical principle

图片选项

0 引言

2008年5· 12汶川发生8.0级特大地震, 在强震区沟道及岸坡两侧产生了大量松散堆积物, 导致西南山区在震后强降雨的激发作用下泥石流灾害频发^[1]。2010年8月13日都江堰龙池地区特大暴雨导致48条泥石流沟同时爆发, 2019年8月20日位于汶川灾区的都江堰受强降雨影响, 暴发群发性山洪泥石流灾害^{[2, 3, 4, 5]}。可见, 震后次生灾害持续效应明显, 震后5~15 a间, 泥石流活动性演化为低频、大中型、群发、黏— 过渡性泥石流并伴有山洪。由于位于流域上游泥石流形成区沟岸两侧的松散物源具有地处高位且储量较小的特点, 在以往研究中常常被忽视, 但其对沟道泥石流的形成具有强烈的放大效应^[6]。一方面, 由于形成区地处流域高位, 具有丰富的松散物源量和较大的沟道纵比降, 使得坡面物源失稳后成为补给物源, 同时裹挟铲刮沟道物源进一步诱发流速较高的沟道泥石流, 具有暴发前隐蔽性强、连锁破坏性大的特点^[7]; 另一方面, 西南山区汛期强降雨爆发, 位于形成区上方的集雨区形成汇流进入沟道需要时间, 形成区坡面物源的失稳会早于沟道泥石流启动10~15 min^[8], 这短短十几分钟足以让危险范围内的百姓提前撤离^[9]。因此, 认识沟源岸坡失稳启动的水动力条件及力学机理对实现沟道泥石流的超前预警预报具有重大的现实意义。

前人对土力类泥石流和水力类泥石流已经进行了较深入的研究^{[10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]}, 对具有松散结构特性岩土体泥石流化的机制也有了初步研究, 然而这些研究并未涉及震后特殊条件下的坡面物源泥石流启动问题, 相关成果无法满足灾后重建对防灾技术的要求。

本文以都江堰银洞子沟为例, 借助水力学理论, 分析泥石流形成区坡面松散堆积体内潜水位随降雨强度的变化规律和特征, 解析震后强降雨条件下坡面物源松散堆积体失稳的力学机制, 并反演降雨阈值及启动的临界条件, 最后与实际监测数据比对验证。通过人工降雨物理模拟实验, 实时监测坡体内潜水位及坡体介质力学参数随雨强变化的响应关系、失稳临界条件及失稳模式。将理论分析、实例验证和物理模拟结果结合, 对坡面松散物源启动力学机理、启动临界条件及启动模式进行深入剖析, 为沟道泥石流启动的超前预警提供参考依据。

1 震后坡面松散堆积体启动力学机制

持续稳态强降雨的激发作用降低了震后坡面松散堆积体的稳定性, 最终导致斜坡表层堆积体转化为固、液、气三相混合的坡面泥石流, 坡面泥石流的启动是复杂水土耦合作用的结果^{[23, 24]}, 需要综合应用土力学、水力学以及渗流力学的理论方能揭示震后坡面松散堆积体转化为泥石流的力学机制。

1.1 强降雨在坡面松散堆积体中形成的潜水层厚度

设稳态暴雨的雨强(单位时间、单位面积降雨量)为 $I$ , 坡体表面积(即集雨面积)为 $S$ , 则入渗至整个坡体的降雨流量为

$Q = IS$ 。 (1)

式中: Q为降雨渗流量, m³/h; I为单位时间、单位面积降雨量, mm· h^-1· m^-2; S为集雨面积, m²。

震后西南山区泥石流形成区的坡面松散堆积体为碎石土, 结构松散且渗透系数大, 汛期暴雨来临, 随强降雨的不断入渗, 基岩面以上饱和土体中产生饱水层厚度为H的自由水头(即一定高度的潜水位), 堆积体受水力作用而失稳, 最终可能转化为泥石流。由可以适用于地下水层流的达西定律可知, 降雨入渗至坡体的渗流流量与上下游的水位差(距离大地水准面的高程之差)和过水断面面积成正比, 与渗流路径的长度呈反比, 公式为

$Q = KA (H_{2} - H_{1}) / L = KA \sin θ$ 。 (2)

式中: $Q$ 为降雨渗流量, m³/h; $K$ 为渗透系数, m/d; $A$ 为垂直于水流方向的截面积(过水断面面积), m²; $H_{2} - H_{1}$ 为上下游的水位差, m; $L$ 为渗流路径的长度, m; $θ$ 为潜水位倾角, (° )。

图1为坡面松散堆积体的水文模型。

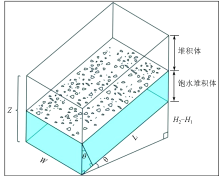	Figure Option View Download New Window
	图1 坡面堆积体的水文模型 Z.坡面松散堆积体铅垂厚度, m; $L$ .渗流路径的长度, m; $θ$ .潜水位倾角, (° ); W.坡体宽度, m; $(H_{2} - H_{1})$ .上下游的水位差, m。Fig.1 The hydraulics model of slope deposit

由该水文模型可得

$A = WH \cos θ$ 。 (3)

式中: $W$ 为坡体宽度, m; $H$ 为潜水层厚度, m。

将式(3)带入式(2)可得

$Q = KWH \cos θ \cdot \sin θ$ 。 (4)

综合式(1)和式(4), 可得

$H = \frac{IS}{KW \sin θ \cdot \cos θ}$ 。 (5)

理论上, 随降雨的持续, 地下水位高度可不断抬升, 直至坡体完全饱和, 即: $H = Z$ (其中 $Z$ 为坡面松散堆积物的铅垂厚度), 最终潜水溢出坡面松散堆积体表面, 在坡体表面形成地表径流或超渗表面流。根据水力学饱和土体中的径流流量表达式可得

$Q_{Z} = T_{D} W \sin θ$ 。 (6)

式中: $T_{D}$ 为导水系数, m²/d。

综合式(4)与式(6), 可得

$K = T / Z \cos θ$ 。 (7)

将式(7)代入式(5), 可将公式简化得到式(8)所示的降雨入渗后坡体内产生的潜水层铅垂厚度

$H = \frac{ISZ}{T_{D} W \sin θ}$ 。 (8)

由式(8)可建立潜水层垂直厚度与降雨雨强、潜水面倾角、坡体面积等几何参数的多元函数关系和模型(图1), 可见潜水层垂直厚度受以上多方面因素的共同作用: 潜水层垂直厚度H与降雨雨强I、坡面松散堆积体铅垂厚度Z呈正比, 与导水系数、坡体宽度和潜水位倾角呈反比, 并且地下水位的深度主要受降雨强度的控制。

1.2 坡面松散堆积体水力作用机制

1.2.1 静水压力作用

如图2所示, 设堆积体条块上端入口处的潜水深度为 $h_{2}$ , 下端出口处的潜水深度为 $h_{1}$ , 建立沿沟床方向为 $X$ 方向、垂直于沟床为 $Y$ 方向的坐标系。由堆积体内一点静水压力 $P_{h} = γ_{w} \cdot h$ (其中 $γ_{w}$ 为堆积体内水的重度, N/m³; $h$ 为这一点之上的自由水深度, 即潜水面到此点的深度, 简称潜水深度, m), 可得沿 $X$ 方向某一点的渗透静水压力为

$P_{X} = P_{h_{1}} + \frac{x}{L} (P_{h_{2}} - P_{h_{1}})$ , $x \in [0, L]$ 。 (9)

	Figure Option View Download New Window
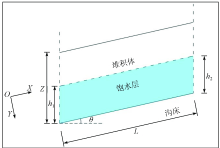	图2 坡面松散堆积体潜水水力作用分析 Z.坡面松散堆积体铅垂厚度, m; $L$ .渗流路径的长度, m; $θ$ .潜水位倾角, (° ); h₁.坡体上部潜水深度, m; h₂.坡体下部潜水深度, m。Fig.2 The hydraulic function analysis of slope loose deposits groundwater level

将m条块的 $P_{m}$ 沿 $X$ 轴积分, 可得该条块堆积体所受静水压力

$\begin{array}{l} P_{m} = \int_{0}^{L} [P_{h_{1}} + \frac{X}{L} (P_{h_{2}} - P_{h_{1}})] d x = \\ \frac{P_{h_{1}} + P_{h_{2}}}{2} L = \\ \frac{γ_{w} (h_{1} + h_{2})}{2} L, x \in [0, L] \end{array}$ 。 (10)

设 $H_{m} = \frac{h_{1} + h_{2}}{2}$ , 则 $H_{m}$ 为该条块堆积体的平均水深, 该条块所受静水压力为

$P_{m} = γ_{w} H_{m} L$ 。 (11)

该静水压力是一种全方位的力, 并均匀地施加在坡面松散堆积体底面的各个部位。堆积体基岩面上潜水流的平均垂直压应力为

$σ_{w m} = γ_{w} H_{m}$ 。 (12)

式中: σ _w_m为平均垂直压应力, Pa。

1.2.2 动水压力作用

震后坡面松散堆积体结构松散, 孔隙大, 颗粒组成以碎石土为主。当汛期雨强足够大, 持续时间足够长时, 堆积体内部会产生一定高度的潜水位, 底部发生层流, 并产生渗流动水压力, 动水压力对土骨架的作用以“ 拖拽” 的形式表现出来。

根据连续介质原理, 渗流区域内任一点所受的渗流动水压力为

$\vec{G_{d}} = γ {\vec{I}}_{w}$ 。 (13)

式中: $\vec{G_{d}}$ 和 $\vec{I_{w}}$ 为动水压力矢量和水力坡降矢量。

则堆积体底部层流对单位宽度坡面堆积体的渗流动水压力为

$G_{d m} = \int_{0}^{H_{m}} \int_{0}^{L} e γ_{w} I d x d y = eL H_{m} γ_{w} I_{m}$ 。 (14)

式中: G_dm为渗流动水压力, N; e为松散堆积物的孔隙比, 无量纲; $I_{m}$ 为单位宽度坡面松散堆积体中潜水的水力坡度, 无量纲。

综合考虑得出

$I_{m} = \frac{h_{2} + L \sin θ - h_{1}}{L}$ 。 (15)

堆积体内的潜水在渗流作用下对坡面堆积体的拖拽力为

$d_{m} = \frac{G_{d m}}{L} = e γ_{w} I_{m} H_{m} = \frac{e γ_{w} H_{m} (h_{2} + L \sin θ - h_{1})}{L}$ 。 (16)

当坡面潜水流经松散堆积体时, 雨水本身的黏滞作用和土颗粒介质对慢速水流的摩擦阻力分别是产生水头损失的主要内因和外因。此时, 如果坡面堆积体的物理性质和渗透性质确定, 则处于低速流动状态的底部层流在单位流动距离上的水头损失 $η$ 是确定的, 并可由响应模型试验得出。

式(14)可简化为

$G_{d m} = λL H_{m} γ_{w} η$ 。 (17)

当然, 对于整个坡面松散堆积体而言, 若潜水水头在流出堆积体前就消失殆尽, 则上述水力作用中渗流动水压力的拖拽作用无法体现出来。假定松散堆积体顶部的自由水头为 $h_{m 1}$ , 整个堆积体被划分为 $m$ 个条块, 则基覆面(基岩与覆盖层的交界面)产生底部层流的条件为

$h_{m 1} + \overset{m = n}{\sum_{m = 1}} L_{m} \sin θ_{m} - \overset{m = n}{\sum_{m = 1}} η L_{m} \geq 0$ 。 (18)

1.3 强降雨条件下坡面松散堆积体的受力及稳定性

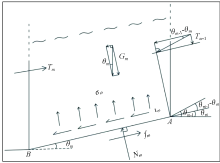
考虑到震后坡面松散堆积体的坡度并非均一, 在进行受力分析时, 可根据底部基岩面的坡度变化, 对坡面松散堆积体进行进一步的精细划分, 从而形成多段单元条块(m=1, 2, …, n), 如图3所示。在不考虑各单元条块之间的剪切错动的条件下, 控制第 $m$ 段坡面松散堆积体稳定性的外力有重力、条块间的剩余下滑力、静水压力、动水压力、基岩面的支持力、基底抗滑力, 若条块下滑力大于抗滑力, 则力系平衡, 堆积体条块稳定。

	Figure Option View Download New Window
	图3 单元松散堆积体条块受力分析示意图 T_m.下一条块反作用力, N; T_m_-1.m-1条块的剩余下滑力, N; G_m.条块m的重力, N; $τ_{w}$ 、 $σ_{w}$ 分别为滑移面上的切应力与正应力, Pa; N_m.条块m的基底反力, N; $f_{m}$ .条块 $m$ 的基底抗滑力, N。Fig.3 The force analysis schematic diagram of the unit loose accumulation body strip

对条块m进行受力分析可得, 该条块沿基岩面AB滑动的下滑力为

$S_{m} = G_{m} \sin θ_{m} + T_{m - 1} \cos (θ_{m - 1} - θ_{m}) + G_{dm}$ 。 (19)

式中: $S_{m}$ 为该条块的下滑力, N; $G_{m}$ 为条块 $m$ 的重力, N; $T_{m - 1}$ 为上一条块 $m - 1$ 的剩余下滑力, N。需要特别说明的是, 当 $m = 1$ 时, 条块为最上方单元条块(初始条块), 不存在上一条块的剩余下滑力 $T_{m - 1}$ ; 同样, 当 $m = n$ 时, 条块为堆积体最下方的单元条块, 不存在下一条块 $m + 1$ 的反作用力 $T_{m}$ , 即

$\{\begin{array}{l} T_{0} = 0, \\ T_{m} = 0 。 \end{array}$ (20)

作用在条块 $m$ 的抗滑力为

$F_{m} = T_{m} + f_{m}$ 。 (21)

式中: $T_{m}$ 为下一条块的反作用力, N; $f_{m}$ 为条块 $m$ 的基底抗滑力, N。

1773年, 库伦提出了摩尔-库伦屈服准则

$τ_{w} = c + σ_{w} \tan φ$ 。 (22)

式中: $c$ 为松散堆积土体的黏聚力, Pa; $φ$ 为松散堆积土体的内摩擦角, (° ); $τ_{w}$ 、 $σ_{w}$ 分别为滑移面上的切应力与正应力, Pa。

结合式(9)静水压力公式可得

$τ_{w} = \frac{f_{m}}{L} = c + \frac{[G_{m} \cos θ_{m} + T_{m - 1} \sin (θ_{m - 1} - θ_{m}) - γ_{w} H_{m} L]}{L} \tan φ$ 。 (23)

简化后, 可得

$\begin{array}{l} f_{m} = cL + [G_{m} \cos θ_{m} + T_{m - 1} \sin (θ_{m - 1} - θ_{m}) - γ_{w} H_{m} L] \tan φ f_{m} = \\ cL + [G_{m} \cos θ_{m} + T_{m - 1} \sin (θ_{m - 1} - θ_{m}) - γ_{w} H_{m} L] \tan φ \end{array}$ 。 (24)

根据堆积体的受力分析可得, 松散堆积体单元条块 $m$ 稳定条件是 $F_{m} \geq S_{m}$ , 在理论上此时条块1至条块 $m$ 都是稳定的。特别是当松散堆积体第 $n$ 个条块抗滑力F_n仍大于下滑力S_n( $F_{n} \geq S_{n}$ )时, 整个堆积体处于整体稳定的状态。反之, 当第 $m$ 单元条块堆积体稳定, 而第 $n$ 个条块不稳定, 则坡面松散堆积体发生部分启动现象, 此时, 第 $n$ 单元条块堆积体也必满足 $F_{n} < S_{n}$ 。

2 监测数据实例

2.1 研究区概况

为验证本文对坡面松散堆积体失稳的水力学机制分析, 以都江堰市银洞子沟^{[25, 26]}作为研究对象进行实例分析。银洞子泥石流沟位于汶川地震重灾区都江堰市龙池镇, 海拔1 070~2 050 m, 属中山峡谷构造侵蚀地貌, 山体走向多为NE— SW向, 山脊狭窄, 一般地形坡度为30° ~55° , 沟谷切割较深, 上陡下缓, 多为“ V” 型谷。

沟域内出露地层为基岩和第四系松散堆积物, 其中基岩为震旦系下统火山岩组(Z_a)的花岗岩、安山岩、闪长岩、凝灰岩及部分变质岩。第四系地层为全新统残坡积( $Q_{4}^{el + pl}$ )、洪坡积( $Q_{4}^{pl + dl}$ )以及崩坡积( $Q_{4}^{col + dl}$ )层, 以松散的宽级配碎石类土为主, 厚度约1~20 m, 变化较大, 一般呈现山脊处薄、沟谷处厚的特点, 沟谷两侧共计5处堆积体, 为泥石流的启动提供了丰富的松散物源。银洞子沟域面积约2.2 km², 主沟整体长2.5 km, 主沟平均纵坡降为310‰ , 沟道总物源量为83.55× 10⁴ m³, 坡面可参与泥石流活动的动储量为23.02× 10⁴ m³(图4)。

	Figure Option View Download New Window
	图4 银洞子泥石流沟地形Fig.4 Topographic map of Yindongzi Debris flow Gully

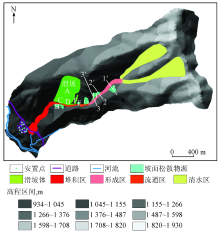
银洞子泥石流沟清水区为三面环山一面出口的漏斗状地形。海拔1 560~1 330 m为形成区, 沟长813 m, 集雨面积0.35 km², 沟谷深切, 地势陡峻, 谷坡45° ~75° , 平均纵坡比降283‰ , 这种地形条件使泥石流得以迅猛直泻, 形成区物源启动早于沟道泥石流暴发, 因此, 将形成区的4个物源松散堆积体作为本研究的重点研究对象, 以实现沟道泥石流启动的超前预警。流通区为汶川大地震的同震滑坡, 堆积区地形坡度7° , 位于银洞子沟沟口, 松散堆积体总量2.8× 10⁴ m³(图5, 图6)。泥石流沟口堆积扇右侧已修建虹口乡联合村灾后重建安置点(图5), 该安置点计划安置56户, 人口228人, 下游紧邻白沙河。

	Figure Option View Download New Window
	图5 沟口堆积扇与灾后重建安置点Fig.5 The accumulation fan in gully mouth and post-disaster reconstruction site

	Figure Option View Download New Window
	图6 研究区坡脚松散堆积体Fig.6 Loose deposits at the foot of slope in the study area

研究区降雨充沛但时空分布不均, 多年平均降雨量约为1 100 mm, 单日最大降雨量为183.2 mm(2010-08-13), 汛期暴雨频繁, 雨量集中, 这为坡面松散堆积体启动提供了水动力条件。泥石流潜在危险性为中等, 对人民的生命财产安全造成了巨大威胁。

2.2 震后坡面松散堆积体启动水力学机制

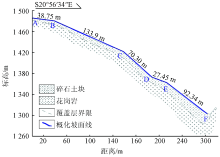
在有关震后坡面松散堆积体启动机制研究开展前, 已对都江堰银洞子泥石流沟进行了详细的野外调查和地质勘查工作, 对全流域进行了精准的测图和探槽开挖, 并在1:1 000的地形图上(图4)对形成区坡面物源的地质地貌要素进行了详细的计算和统计, 探明了松散物源堆积体的分布、储量、形态等特征要素。为研究震后松散堆积体在降雨激发作用下启动的模式和条件, 现对位于形成区上方剖面3-3’ 所在坡面(图7, 图8)进行受力分析。经现场地质调查表明, 坡体宽为23.07~115.96 m, 斜长326.7 m, 面积约5 000 m², 坡度为8.16° ~45.34° , 坡体多为松散的滑坡堆积体, 呈上薄下厚分布, 目前处于欠稳定状态。根据该堆积体的剖面图(图7), 可按平均宽度、坡度、堆积厚度从上至下划分为5段: AB、BC、CD、DE和EF, 如图7、图8所示。相关计算参数如表1、表2所示。

	Figure Option View Download New Window
	图7 剖面3-3’ 松散堆积体剖面Fig.7 The loose deposits cross section diagram of section plane 3-3’

	Figure Option View Download New Window
	图8 坡面松散堆积体的条块划分 AB区对应剖面AB段; BC区对应剖面BC段; CD区对应剖面CD段; DE区对应剖面DE段; EF区对应剖面EF段。Fig.8 Strip division of slope loose deposits

表1 H滑坡坡面松散堆积体的几何参数 Tab.1 The slope loose deposits Geometric parameters of H landslide

阶段	L_m/m	W_m/m	Z_m/m	$θ_{m} / (°)$
AB	38.75	23.07	5.50	8.16
BC	133.90	42.33	60.00	26.62
CD	70.30	66.15	50.00	45.34
DE	27.45	87.83	10.50	22.49
EF	92.34	115.96	60.50	40.93

表1 H滑坡坡面松散堆积体的几何参数 Tab.1 The slope loose deposits Geometric parameters of H landslide

表2 震后坡面松散堆积体的力学参数 Tab.2 Mechanical parameters of post-earthquake slope loose deposits

内摩擦角( $φ$ )/( $°$ )	堆积体孔隙比 $(λ)$	单位长度水头损失 $(η)$	黏聚力(c)/kPa	导水系数(T_D)/ (m²· h^-1)	堆积体重度( $γ$ _s)/ (kN· m^-3)	潜水重度( $γ$ _w)/ (kN· m^-3)
34.1	0.42	0.24	10.15	301	18.9	9.8

表2 震后坡面松散堆积体的力学参数 Tab.2 Mechanical parameters of post-earthquake slope loose deposits

2.2.1 降雨导致的坡面松散堆积体内潜水位高度与水力条件变化规律

将研究区坡面松散堆积体的几何与力学参数(表1, 表2)代入式(8), 可计算出不同稳态降雨强度对应的坡面各段堆积体的潜水层铅垂厚度。需要说明的是, 根据坡体平均坡度, 3-3’ 坡面被划分为5段, 第1段堆积体位于坡面顶部, 集雨面积为该段接受降雨面积, 第2段堆积体的集雨面积为上一堆积体集雨面积与本段坡面堆积体面积之和, 以此类推。根据降雨强度, 等级可划分为: 小雨(< 10 mm/d)、中雨(10~25 mm/d)、大雨(25~50 mm/d)、暴雨(50~100 mm/d)、大暴雨(100~250 mm/d)、特大暴雨(> 250 mm/d), 图9所示为不同稳态降雨强度对应的各坡段堆积体的潜水层铅垂厚度。

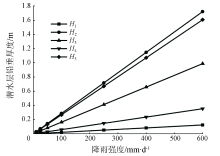	Figure Option View Download New Window
	图9 不同雨强对应的各坡段坡面堆积体中的潜水层铅垂厚度Fig.9 The plumb thickness of groundwater aquifer of slope accumulation body at different positions relative to different rain intensity

理论上, 随降雨强度增大, 堆积体内潜水层铅垂厚度 $H$ 也就越大, 直到超出堆积体厚度溢出坡体表面形成地表径流。但实际上由于研究区坡面堆积体厚度较大, 即使发生特大暴雨(雨强为600 mm/d), 也不会出现潜水溢出的情况。堆积体坡度越小, 坡面越窄, 堆积体越厚, 则潜水位高度越高, 其中, 集雨面积的影响最大。由于第2坡段堆积体坡面斜长BC最大, 从而集雨面积很大, 因此, 第2坡段堆积体中产生了最高的潜水位; 而具有最小集雨面积的第1坡段堆积体AB产生了最低的潜水位。其次, 潜水位高度对坡度的敏感性也很强, 这就导致了具有最大坡度的第3坡段和第5坡段堆积体CD和EF均产生了较大的潜水层铅垂厚度。

不同降雨强度导致的坡面松散堆积体内潜水层铅垂厚度不同, 从而所受到的水力作用也是变化的。由式(16)可知, 堆积体内产生的潜水会发生“ 层流” , 渗流的动水压力以“ 拖拽” 的形式表现出来, 整个堆积体动水压力远小于静水压力(图10)。这说明震后坡面松散堆积体在降雨中失稳主要是潜水位抬升、静水压力变化的结果。随雨强持续增大, 理论上直到潜水溢出坡面后, 坡面松散堆积体中动静水压力等水力条件才会保持恒定不变。

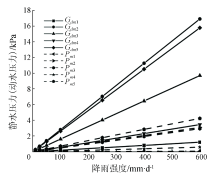	Figure Option View Download New Window
	图10 不同降雨导致的坡面堆积体水力条件变化规律Fig.10 Hydraulic variation rual of slope accumulation body under different rainfall conditions

2.2.2 震后坡面松散堆积体启动受力分析

根据1.3中的坡面松散堆积体受力稳定性分析, 现对都江堰银洞子沟坡面松散堆积体启动的临界条件、启动模式和稳定性进行分析计算。若剩余下滑力为负值, 表明该段堆积体可以自稳, 并余有抗滑储备, 此时堆积体稳定, 对下一段堆积体的作用力记为0。

计算结果(表3, 表4)表明: 第1坡段坡面松散堆积体在特大暴雨的降雨条件下, 剩余下滑力仍为负值, 说明这段堆积体可自稳, 不会启动, 也不能作为补给沟道物源的动储量。降雨强度与坡度对坡面松散堆积体稳定性的影响最大, 对同一坡段松散堆积体而言, 雨强越大, 下滑力越大, 抗滑力由于自重增加而持续增大, 但增速小于下滑力, 导致剩余下滑力逐渐增大。坡度对坡面松散堆积体稳定性的影响最敏感, 参照表1所列各坡段的坡度, 第3坡段堆积体与第5坡段堆积体坡度均大于40° , 即使受到的的雨强很小也很难实现自稳。第4坡段堆积体的坡度又放缓(22.49° ), 导致剩余下滑力处于第3坡段和第4坡段之间, 说明第4坡段抵抗了一部分来自于上一坡段堆积体的推移力。

表3 不同雨强下堆积体各段剩余下滑力 Tab.3 Stress values of accumulation bodies in different rainfall conditions

表4 不同雨强条件下各块体下滑力及基地抗滑力 Tab.4 Residual sliding force under different rainfall conditions

当剩余下滑力 $T$ 为负值时, 表明堆积体自身可稳定, 对下一堆积体无力的作用。

由于剩余下滑力差值较小, 为直观体现其变化规律, 采用剩余下滑力差值D(即剩余下滑力与本组剩余下滑力最小值之差)表现剩余下滑力的变化, 图11所示除 $T_{1}$ 为第1坡段堆积体的剩余下滑力外, 其剩余坡段均为剩余下滑力差值。

	Figure Option View Download New Window
	图11 不同降雨强度对应的坡面松散堆积体剩余下滑力变化规律Fig.11 Variation law of residual sliding force of slope accumulation body relative to rainfall intensity

图11、表3、表4揭示了不同降雨强度对应的不同坡段松散堆积体下滑力、抗滑力与剩余下滑力的变化规律。第1坡段堆积体在任何降雨条件下都能实现自稳, 第2~5坡段堆积体极不稳定, 遭受很小的雨强即可丧失抗滑储备, 导致第2~5段堆积体接连整体失稳, 这种启动方式为典型的推移式失稳。理论上, 若第 $m$ 坡段堆积体稳定, 而第( $m + 1$ )坡段堆积体启动, 则坡面松散堆积体就会以解体的方式分段启动并泥石流化, 这是典型的牵引式失稳。

4 结论

(1)震后坡面松散堆积体组成主要为碎石土, 具有宽级配和渗透系数大等特点, 坡面松散堆积体启动失稳是在强降雨激发作用下, 坡体内潜水位不断升高, 水力条件不断恶化的结果。

(2)根据水力学、土力学等理论分析, 堆积体内潜水层铅垂厚度H与坡面面积S、稳态降雨强度 $I$ 、坡面堆积体几何形态、导水系数 $T_{D}$ 等因素密切相关。对于具有一定物理力学性质和几何状态的坡面堆积体而言, 坡面面积(聚水面积) $S$ 、降雨强度 $I$ 越大, 则潜水层铅垂厚度 $H$ 越大; 对于一定的坡面集雨面积和稳态激发降雨强度, $T_{D}$ 、 $W$ 、 $θ$ 越大, $Z$ 越小, 则坡面堆积体体内产生潜水层铅垂厚度越小。总而言之, 坡面越窄, 堆积体厚度越大, 坡面面积越大, 坡面松散堆积体越容易失稳并进一步泥石流化。

(3)潜水位抬升会产生2种水力作用: 一方面, 坡体内静水压力 $P_{m}$ 增高, 降低了堆积体基底抗滑力; 另一方面, 动水压力 $G_{d}$ 的增高, 增加了坡体启动的下滑力, 然而动水压力在松散堆积体雨后失稳的作用相对较小。

(4)根据剩余下滑力的存在形式, 震后坡面松散堆积体的启动模式可分为2种: 坡体整体启动的推移式失稳; 分段解体启动的牵引式失稳。对研究区银洞子泥石流沟3— 3’ 剖面坡面松散堆积体的分析表明, 除处于最高位置的第1坡段堆积体可自稳外, 第2~5坡段堆积体剩余下滑力不断向下累积, 呈现整体推移式失稳的启动模式。

(责任编辑: 常艳)

参考文献

文献选项

[1]	吕小波, 游勇, 柳金峰, 等. 汶川2019年“8·20”群发性泥石流降雨特征与临界雨量分析[J]. 兰州大学学报: 自然科学版, 2021, 57(6): 775-782, doi: 1013885/j. issn. 0455-2059. 2021. 06. 009. Lv X B, You Y, Liu J F, et al. Rainfall characteristics and rain threshold of Wenchuan debris flows on August 20, 2019[J]. J Lanzhou Univ: Nat Sci, 2021, 57(6): 775-782, doi: 10.13885/j.issn.0455-2059.2021.06.009. [本文引用:1]
[2]	靳文, 张国涛, 邹强, 等. 震后泥石流活跃期的新认识——以四川汶川“8·20”灾害事件为例[J]. 山地学报, 2019, 37(5): 787-796, doi: 1016089/j.cnki.1008-2786.000469. Jin W, Zhang G T, Zou Q, et al. A new understand ing of the activity behavior of post-earthquake debris flow: Taking the “8·20” event in Wenchuan, Sichuan, China as an example[J]. Mount Res, 2019, 37(5): 787-796, doi: 10.16089/j.cnki.1008-2786.000469. [本文引用:1]
[3]	余斌, 杨凌崴, 刘清华, 等. 基于沟床宽度与颗粒粒径的泥石流精细化预报模型[J]. 地球科学, 2020, 45(4): 1447-1456, doi: 103799/dqkx.2019.131. Yu B, Yang L W, Liu Q H, et al. A precise prediction model on debris flows caused by runoff mechanism based on channel width and particle size[J]. Earth Sci, 2020, 45(4): 1447-1456, doi: 10.3799/dqkx.2019.131. [本文引用:1]
[4]	李奋生, 李勇, 赵国华, 等. 汶川8. 0级地震震后泥石流空间分布和控制因素分析[J]. 灾害学, 2014, 29(2): 38-41, doi: 103969/j.issn.1000-811X.2014.02.009. Li F S, Li Y, Zhao G H, et al. Space distribution and control factors of debris flows after Wenchuan M8. 0 earthquake[J]. J Catastrophol, 2014, 29(2): 38-41, doi: 10.3969/j.issn.1000-811X.2014.02.009. [本文引用:1]
[5]	雷发洪, 胡凯衡, 胡云华, 等. 汶川地震灾区震后泥石流激发雨量研究[J]. 灾害学, 2014, 29(2): 199-203, doi: 103969/j.issn.1000-811X.2014.02.037. Lei F H, Hu K H, Hu Y H, et al. Excitation rainfall of debris flows in the stricken area of Wenchuan earthquake[J]. J Catastrophol, 2014, 29(2): 199-203, doi: 10.3969/j.issn.1000-811X.2014.02.037. [本文引用:1]
[6]	潘华利, 安笑, 邓其娟, 等. 泥石流松散固体物源研究进展与展望[J]. 科学技术与工程, 2020, 20(24): 9733-9741. Pan H L, An X, Deng Q J, et al. Progress and prospects of research on debris flow solid source[J]. Sci Technol Eng, 2020, 20(24): 9733-9741. [本文引用:1]
[7]	吴永, 何思明, 裴向军, 等. 震后沟道泥石流启动条件——松散堆积体雨中失稳的水力学机制分析[J]. 岩土力学, 2012, 33(10): 3043-3050, doi: 1016285/j.rsm.2012.10015. Wu Y, He S M, Pei X J, et al. Analysis of condition of startup of gully debris flow after earthquake-the hydraulic mechanism of instability of loose deposits in rainfall[J]. Rock Soil Mechan, 2012, 33(10): 3043-3050, doi: 10.16285/j.rsm.2012.10.015. [本文引用:1]
[8]	Ouyang C J, An H C, Zhou S, et al. Insights from the failure and dynamic characteristics of two sequential land slides at Baige village along the Jinsha River, China[J]. Land slides, 2019, 16(7): 1397-1414, doi: 10.1007/s10346-019-01177-9. [本文引用:1]
[9]	胡涛. 汶川震区震后大型泥石流致灾机理及防治对策研究[D]. 成都: 成都理工大学, 2017. Hu T. The Research on Formation Mechanism and Mitigation Measures of Large-scale Debris Flow in the Wenchuan Earthquake Area[D]. Chengdu: Chengdu University of Technology, 2017. [本文引用:1]
[10]	Shieh C L, Chen Y S, Tsai Y J, et al. Variability in rainfall threshold for debris flow after the Chi-Chi earthquake in central Taiwan, China[J]. Int J Sedim Res, 2009, 24(2): 177-188, doi: 10.1016/S1001-6279(09)60025-1. [本文引用:1]
[11]	Johnson K A, Sitar N. Hydrologic conditions leading to debris-flow initiation[J]. Canad Geotechn J, 1990, 27(6): 789-801. [本文引用:1]
[12]	Marchi L, Arattano M, Deganutti A M. Ten years of debris-flow monitoring in the Moscardo Torrent (Italian Alps)[J]. Geomorphology, 2002, 46(1/2): 1-17, doi: 10.1016/S0169-555X(01)00162-3. [本文引用:1]
[13]	黄海, 石胜伟, 杨顺, 等. 2017年“8·8”九寨沟地震对景区泥石流治理工程影响机制研究[J]. 岩石力学与工程学报, 2020, 39(9): 1773-1786, doi: 1013722/j.cnki.jrme.2020.0099. Huang H, Shi S W, Yang S, et al. Study on the damage of the August 8, 2017 Jiuzhaigou earthquake to debris flow mitigation engineering in the national park[J]. Chin J Rock Mechan Eng, 2020, 39(9): 1773-1786, doi: 10.13722/j.cnki.jrme.2020.0099. [本文引用:1]
[14]	Wen B P, Aydin A. Mechanism of a rainfall-induced slide-debris flow: constraints from microstructure of its slip zone[J]. Eng Geol, 2005, 78(1/2): 69-88. [本文引用:1]
[15]	高冰, 周健, 张姣. 泥石流启动过程中水土作用机制的宏细观分析[J]. 岩石力学与工程学报, 2011, 30(12): 2567-2573. Gao B, Zhou J, Zhang J. Macro-meso analysis of water-soil interaction mechanism of debris flow starting process[J]. Chin J Rock Mechan Eng, 2011, 30(12): 2567-2573. [本文引用:1]
[16]	朱颖彦, 崔鹏, 陈晓晴. 泥石流堆积体边坡失稳机理的试验与稳定性分析[J]. 岩石力学与工程学报, 2005, 24(21): 3927-3934. Zhu Y Y, Cui P, Chen X Q. Experiment on mechanism of slope failure of debris flow fan and stability analysis[J]. Chin J Rock Mechan Eng, 2005, 24(21): 3927-3934. [本文引用:1]
[17]	游勇, 柳金峰, 欧国强. 泥石流常用排导槽水力条件的比较[J]. 岩石力学与工程学报, 2006, 25(S1): 2820-2825. You Y, Liu J F, Ou G Q. Comparison of hydraulic conditions among usual debris flow drainage canal[J]. Chin J Rock Mechan Eng, 2006, 25(S1): 2820-2825. [本文引用:1]
[18]	Cui P. Study on conditions and mechanisms of debris flow initiation by means of experiment[J]. Chin Sci Bull, 1992, 37(9): 759-763. [本文引用:1]
[19]	杨顺, 欧国强, 王钧, 等. 恒定渗流作用下泥石流起动过程冲刷试验分析[J]. 岩土力学, 2014, 35(12): 3489-3495, doi: 1016285/j.rsm.2014.12.019. Yang S, Ou G Q, Wang J, et al. Experimental analysis of scouring of debris flow initiation process under steady seepage condi-tion[J]. Rock Soil Mechan, 2014, 35(12): 3489-3495, doi: 10.16285/j.rsm.2014.12.019. [本文引用:1]
[20]	Guo C X, Cui Y F. Pore structure characteristics of debris flow source material in the Wenchuan earthquake area[J]. Eng Geol, 2020, 267: 105499, doi: 10.1016/j.enggeo.2020.105499. [本文引用:1]
[21]	Cui Y F, Zhou X J, Guo C X. Experimental study on the moving characteristics of fine grains in wide grading unconsolidated soil under heavy rainfall[J]. J Mount Sci, 2017, 14(3): 417-431, doi: 10.1007/s11629-016-4303-x. [本文引用:1]
[22]	Yang Z J, Cai H, Shao W, et al. Clarifying the hydrological mechanisms and thresholds for rainfall-induced land slide: in situ monitoring of big data to unsaturated slope stability analysis[J]. Bull Eng Geol Environ, 2019, 78(4): 2139-2150, doi: 10.1007/s10064-018-1295-5. [本文引用:1]
[23]	徐辉, 张少杰, 黎力, 等. 基于水土耦合物理机制的区域滑坡概率预报技术研究[J]. 灾害学, 2019, 34(4): 86-91, doi: 103969/j.issn.1000-811X.2019.04.016. Xu H, Zhang S J, Li L, et al. Research on physics-based probabilistic forecasting technology of regional land slide[J]. J Catastrophol, 2019, 34(4): 86-91, doi: 10.3969/j.issn.1000-811X.2019.04.016. [本文引用:1]
[24]	龚凌枫, 唐川, 李宁, 等. 急陡沟道物源起动模式及水土耦合破坏机制分析[J]. 地球科学进展, 2018, 33(8): 842-851, doi: 1011867/j.Issn.1001-8166.2018.08.0842. Gong L F, Tang C, Li N, et al. Source inition pattern and coupling mechanism of granular deposit and seepage in steep longitudinal gully, Wenchuan[J]. Adv Earth Sci, 2018, 33(8): 842-851, doi: 10.11867/j.Issn.1001-8166.2018.08.0842. [本文引用:1]
[25]	杨宗佶, 王礼勇, 石莉莉, 等. 降雨滑坡多指标监测预警方法研究[J]. 岩石力学与工程学报, 2020, 39(2): 272-285, doi: 1013722/j.cnki.jrme.2019.0354. Yang Z J, Wang L Y, Shi L L, et al. Research of monitoring and early warning methods for rainfall-induced land slides based on multivariate thresholds[J]. Chin J Rock Mechan Eng, 2020, 39(2): 272-285, doi: 10.13722/j.cnki.jrme.2019.0354. [本文引用:1]
[26]	赵高文, 王萌, 杨宗佶, 等. 震后泥石流沟内滑坡堰塞坝的侵蚀特征分析——以银洞子堰塞坝为例[J]. 工程科学与技术, 2019, 51(5): 68-77, doi: 1015961/j.jsuese.201800571. Zhao G W, Wang M, Yang Z J, et al. Eroding characteristics of land slide dams in debris flow gullies after earthquakes: A case study of Yindongzi Land slide dam[J]. Adv Eng Sci, 2019, 51(5): 68-77, doi: 10.15961/j.jsuese.201800571. [本文引用:1]

2021

0.0

... 0级特大地震,在强震区沟道及岸坡两侧产生了大量松散堆积物,导致西南山区在震后强降雨的激发作用下泥石流灾害频发^[1] ...

2019

0.0

... 2010年8月13日都江堰龙池地区特大暴雨导致48条泥石流沟同时爆发,2019年8月20日位于汶川灾区的都江堰受强降雨影响,暴发群发性山洪泥石流灾害^[2,3,4,5] ...

2020

0.0

2014

0.0

2014

0.0

2020

0.0

... 由于位于流域上游泥石流形成区沟岸两侧的松散物源具有地处高位且储量较小的特点,在以往研究中常常被忽视,但其对沟道泥石流的形成具有强烈的放大效应^[6] ...

2012

0.0

... 一方面,由于形成区地处流域高位,具有丰富的松散物源量和较大的沟道纵比降,使得坡面物源失稳后成为补给物源,同时裹挟铲刮沟道物源进一步诱发流速较高的沟道泥石流,具有暴发前隐蔽性强、连锁破坏性大的特点^[7] ...

2019

0.0

... 另一方面,西南山区汛期强降雨爆发,位于形成区上方的集雨区形成汇流进入沟道需要时间,形成区坡面物源的失稳会早于沟道泥石流启动10~15 min^[8],这短短十几分钟足以让危险范围内的百姓提前撤离^[9] ...

2017

0.0

2009

0.0

... 前人对土力类泥石流和水力类泥石流已经进行了较深入的研究^{[10,11,12,13,14,15,16,17,18,19,20,21,22]},对具有松散结构特性岩土体泥石流化的机制也有了初步研究,然而这些研究并未涉及震后特殊条件下的坡面物源泥石流启动问题,相关成果无法满足灾后重建对防灾技术的要求 ...

1990

0.0

2002

0.0

2020

0.0

2005

0.0

2011

0.0

2005

0.0

2006

0.0

1992

0.0

2014

0.0

2020

0.0

2017

0.0

2019

0.0

2019

0.0

... 1 震后坡面松散堆积体启动力学机制持续稳态强降雨的激发作用降低了震后坡面松散堆积体的稳定性,最终导致斜坡表层堆积体转化为固、液、气三相混合的坡面泥石流,坡面泥石流的启动是复杂水土耦合作用的结果^[23,24],需要综合应用土力学、水力学以及渗流力学的理论方能揭示震后坡面松散堆积体转化为泥石流的力学机制 ...

2018

0.0

2020

0.0

... 1 研究区概况为验证本文对坡面松散堆积体失稳的水力学机制分析,以都江堰市银洞子沟^[25,26]作为研究对象进行实例分析 ...

2019

0.0

... 1 研究区概况为验证本文对坡面松散堆积体失稳的水力学机制分析,以都江堰市银洞子沟^[25,26]作为研究对象进行实例分析 ...