引用本文
杨明钰, 陈红旗, 祁小博, 邹宗山, 王光兵, 刘红岩. 基于可靠度理论的地震滑坡运动距离预测模型[J].中国地质调查, 2023,10(3): 102-109.
YANG Mingyu, CHEN Hongqi, Qi Xiaobo, ZOU Zongshan, WANG Guangbing, LIU Hongyan. Prediction model for the landslide movement distance induced by earthquake based on the reliability theory[J].Geological Survey of China, 2023,10(3): 102-109.  
doi: 10.19388/j.zgdzdc.2023.03.12
Permissions
Copyright@2023, 《中国地质调查》编辑部
《中国地质调查》编辑部 所有
基于可靠度理论的地震滑坡运动距离预测模型
杨明钰1, 陈红旗2, 祁小博2, 邹宗山3, 王光兵3, 刘红岩4
1.中国有色金属工业西安勘察设计研究院有限公司,陕西 西安 710054
2.自然资源部地质灾害应急技术指导中心,北京 100081
3.保利民爆哈密有限公司,新疆 哈密 839000
4.中国地质大学(北京)工程技术学院,北京 100083
通讯作者简介: 刘红岩(1975—),男,教授,主要从事岩体力学及地质灾害方面的教研工作。Email: lhyan1204@126.com。

第一作者简介: 杨明钰(1970—),男,高级工程师,主要从事岩土工程方面的研究与设计工作。Email: 413051472@qq.com。

收稿日期: 2023-02-14 修回日期: 2023-04-13
基金资助: 中国地质调查局“国家级地质灾害应急防治项目(编号: 2022)”和巴里坤县科技局“新疆自治区哈密市巴里坤县科技计划项目”联合资助
摘要

滑坡运动距离是评价滑坡致灾范围的一个重要指标,因此其预测方法一直备受关注。实际滑坡运动距离往往具有很强的随机性,而目前的预测模型往往给出一个确定性的计算公式,未考虑其随机性。基于此,首先,通过对前人提出的基于能量守恒原理的滑坡运动距离理论模型进行分析,认为滑坡运动距离与滑坡体积 V和滑坡前后缘高差 H成正相关,由此提出滑坡运动距离的一般函数关系式; 其次,基于“5·12”汶川地震诱发的46个滑坡案例,对影响滑坡运动距离的主要因素进行了相关性分析,认为滑坡体积 V、滑坡前后缘高差 H及其组合 VH对滑坡运动距离影响显著,并由此建立了滑坡运动距离的多元回归统计模型; 最后,根据工程重要性的不同,在上述研究的基础上提出了基于可靠度理论的滑坡运动距离统计模型。算例分析表明,置信度越高,滑坡运动距离预测范围就越大,相应的搬迁和防护费用就越高,因此应根据实际情况,选择合理的置信度。研究成果有助于进一步优化滑坡运动距离预测的统计模型,进而为滑坡灾害评估和防治提供可靠依据。

关键词: 滑坡; 运动距离; 预测模型; 多元回归分析; 可靠度
中图分类号:P694 文献标志码:A 文章编号:2095-8706(2023)03-0102-08
Prediction model for the landslide movement distance induced by earthquake based on the reliability theory
YANG Mingyu1, CHEN Hongqi2, Qi Xiaobo2, ZOU Zongshan3, WANG Guangbing3, LIU Hongyan4
1. Xi’an Engineering Investigation and Design Research Institute of China Nonferrous Metals Industry Co., Ltd., Shanxi Xi’an 710054,China
2. Geological Disaster Emergency Technical Guidance Center of MNR, Beijing 100081, China
3. Poly Explosive Hami Co., Ltd., Xinjiang Hami, 839000, China
4. School of Engineering and Technology, China University of Geosciences (Beijing), Beijing 100083, China
Abstract

The landslide movement distance is an important index to evaluate the scope of landslide hazard, therefore its prediction method is always being concerned. The actual landslide movement distance often has a strong randomness, but a deterministic calculation formula is offered in current prediction models without the consideration of the randomness. Based on this situation, Firstly, the theoretical model for the landslide movement distance proposed by predecessors was analyzed, and the landslide movement distance is mainly positively correlated with the landslide volume V and elevation H. Then, the authors proposed the general functional relation for the landslide movement distance. Secondly, based on 46 landslide cases induced by “5·12” Wenchuan Earthquake, the correlation analysis of the main factors affecting the landslide movement distance was carried out. It is concluded that the landslide volume V, elevation H and their combination VH have significant influence on the landslide movement distance, and the multiple regression statistical model for the landslide movement distance was established. Finally, the statistical model for the landslide movement distance based on the reliability theory was put forward, according to different engineering importance. The calculation example shows that the higher the confidence is, the larger the predicted range of the landslide movement distance will be, with the higher the relocation and protection cost. Therefore, a reasonable degree of confidence should be chosen according to the actual situation. This study is helpful to further optimize the statistical model for the prediction of the landslide movement distance, and then provides reliable evidence for landslide disaster evaluation and control.

Keyword: landslide; movement distance; prediction model; multiple regression analysis; reliability
0 引言

强震触发的滑坡往往规模大、运动距离远, 因此易造成巨大的人员伤亡和财产损失, 同时还会破坏生态环境, 引起严重的次生灾害。如由2008年汶川地震触发的大光包滑坡, 滑坡体积达7.42亿m3, 造成的堰塞坝高达690 m, 同时还造成了38人死亡、一座磷矿厂和一家伐木厂被摧毁的严重后果[1]。因此, 如何根据滑坡本身特征及场地条件准确预测滑坡运动特征如运动距离、速度等对防灾减灾具有重要指导意义[2]。滑坡沿纵向方向的运动距离在很大程度上决定了滑坡失稳后的致灾范围, 因而备受关注[3, 4]。

目前对滑坡运动距离(由于在实际工程中最关注的是滑坡失稳后的最大运动距离, 因此本文中的运动距离即指最大运动距离)的预测方法主要有以下4类。①理论模型。Scheidegger[5]根据能量守恒原理提出了滑体运动距离预测的摩擦模型, 而后Sassa[6]在此基础上引入了孔隙水压力的影响。然而Helm发现远程滑坡的实际运动距离要远大于摩擦模型的计算结果, 由此提出了滑坡运动距离预测的雪橇模型[7]。王家鼎等[8]结合1920年海原地震诱发的黄土滑坡运动距离统计结果, 通过动力变形分析推导出了黄土滑坡运动距离计算公式。②统计模型。樊晓一[9]通过对众多实际滑坡运动距离的统计分析, 采用多元线性及非线性回归方法提出滑坡运动距离的统计模型。刘红岩等[7]在现有统计模型基础上, 通过引入滑坡前后缘最大落差对其进行修正, 提高了预测精度。③信息模型。王鼐等[10]在对实际黄土滑坡运动距离进行调查的基础上, 采用模糊信息优化处理技术提出了相应的滑坡运动距离预测方法。基于海原地震诱发黄土滑坡运动距离的实测数据, 常晁瑜等[11]建立了地震诱发黄土滑坡运动距离的BP神经网络预测模型。④数值模型。近些年来数值模拟方法被越来越多地用于滑坡运动距离的计算分析, 如: Nian等[12]采用改进的非连续变形分析数值计算程序模拟了汶川地震诱发的大光包滑坡运动距离; Mao等[13]采用离散元数值计算程序模拟了金沙江白格滑坡的滑动距离; Liu等[14]采用PFC程序模拟了四川新茂滑坡的坡体分解、沿程刮铲、碎屑流动和堆积等失稳运动过程, 并给出了滑坡运动距离。

理论模型的理论基础是能量守恒定律和牛顿运动学原理, 多适用于某一个具体滑坡的运动距离预测, 且模型在建立过程中均会采用一定的假设, 因而可能会出现理论预测结果与实际不甚符合的情况; 统计模型和信息模型往往是通过对大量滑坡案例的宏观调查与统计分析, 研究其与滑坡本身及外界作用因素之间的相关关系, 进而获得相应的统计规律和信息, 因而有可能得出与基本物理规律相悖的经验公式, 同时该方法需要以大量已有的滑坡案例为基础; 数值模型是基于数学物理模型而来, 它能很好地模拟整个滑坡的失稳运动过程, 较适合于单体滑坡预测, 但是由于存在计算参数选取困难、计算过程耗时长及技术门槛高等缺点而限制了其推广应用。总之, 上述方法都存在一定的优缺点, 在实际工程中应充分利用各自的优势以更准确、方便地对滑坡运动距离进行预测。

近期地质灾害应急防治已被提上日程[15], 时间紧迫, 任务艰巨, 需要针对某一滑坡的具体情况及时给出滑坡失稳后的可能致灾范围, 进而为人员撤离及财产转移提供指导建议。在此情景下, 统计模型的优势就显得十分突出, 因为对于滑坡特征和诱发因素等内、外因相近的“ 同类” 滑坡而言, 统计模型具有精度高、速度快等特点, 符合地质灾害应急防治需求。但是由于其缺乏相应的滑坡运动力学基础, 会出现得到的统计公式与运动力学机制相悖的情况。同时其未考虑被保护物的重要程度, 导致很难达到安全性与经济性的最佳统一。为此, 本文首先对滑坡运动的力学机制进行分析, 确定统计公式的一般形式; 进而通过参数相关性分析探究对滑坡运动距离影响显著的主要参数, 并基于滑坡案例和多元回归分析方法建立相应的统计模型; 最后, 根据工程重要性, 采用可靠度理论, 提出不同置信度时的滑坡运动距离预测公式。本研究旨在进一步优化滑坡运动距离预测统计模型, 为滑坡灾害评估和防治提供可靠依据。

1 基于能量守恒的滑坡运动距离理论模型

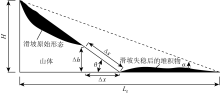
Scheidegger[5]基于能量守恒的观点提出了滑坡运动的摩擦模型, 如图1所示。假设滑坡体质量为m, 沿坡面的运动距离为Δ s, 那么根据能量守恒, 滑坡运动过程中某一时刻的动能变化则等于滑坡重力势能的变化减去克服滑面摩擦力所做的功, 即

Δ12m·v2=m·g·Δh-m·g·cosθ·f·Δs。(1)

式中: v为滑坡运动过程中某一时刻的速度, m/s; f为滑面摩擦系数; g为重力加速度, m/s2; 其余参数含义如图1所示。

图1 滑坡运动距离计算模型
H.滑坡前后缘高差, m; Lr.滑坡运动距离, m; θ .边坡初始倾角, (° ); α .架空坡倾角, (° ); Δ s, 某一滑体沿坡面的运动距离, m; Δ h.某一滑体沿垂直方向的运动距离, m; Δ x.某一滑体沿水平方向的运动距离, mFig.1 Calculation model for the landslide movement distance

对式(1)进行积分, 且认为滑坡启动时初速度及滑坡停止时的最终速度均为0, 则有

0=H-f·Lr⇒f=H/Lr=tanα⇒Lr=H/f。(2)

式中: H/Lr为滑坡失稳前后的前后缘连线斜率, 因此f又称为等效摩擦系数、动摩擦系数或架空坡斜率, 表示滑坡势能转化为克服摩擦力所做的功。

由式(2)可知, 若已知滑坡前后缘高差H和等效摩擦系数f, 则可以求得滑坡运动距离Lr。因此, 其与边坡初始倾角θ 、滑坡体积V及滑坡平均速度等均无关。

然而通过对大量灾难性滑坡的调查研究发现[7], 等效摩擦系数f并非定值, 而是随着滑坡体积的增加而逐渐减小的, 即滑坡水平运动距离是随滑坡体积的增加而增加的。而Scheidegger[5]则认为当滑坡体积V≥ 10万m3时, f随滑坡体积的增加而减小, 否则, 认为其基本不变。由此可知, 滑坡运动距离是受滑坡体积影响的, 而并非无关。这是因为式(1)所示计算方法是基于刚体力学的牛顿运动定理得出的, 而滑坡体并非理想刚体, 其在运动过程中往往会发生碎裂、停积等导致滑坡在运动过程中质量和体积发生变化, 因此式(1)的计算存在较大误差。而实际滑坡运动距离计算方法仍需在式(1)的基础上结合实测数据进行深入研究。

同时其他学者也从不同角度对该问题进行了深入研究, 如郑光等[16]从能量守恒的观点出发, 同时将滑坡体视为刚体, 认为滑坡从开始滑动到最后停止, 滑坡的重力势能全部转化为克服摩擦力所做的功, 即

mgH=ρgVH=FLr。(3)

式中: m为滑坡体质量, kg; H为滑坡前后缘高差, m; F为滑坡体与地面之间的摩擦力等阻力, N; Lr为滑坡运动距离, m; V为滑坡体积, m3; ρ 为滑坡体密度, kg/m3; g为重力加速度, m/s2。

一般来说, 滑坡体的密度变化不大, 即可认为ρ 不变, 同时若认为F也不变的话, 那么滑坡运动距离Lr将与其势能成正比, 即: Lr∝ VH。

而实际滑坡体并非刚体, 通常在滑坡启动后, 成为碎屑流, 相应地摩擦力F也并非常量, 而是与内因(滑坡体特征等)和外因(场地条件等)密切相关, 难以被准确量化。为此, 其将式(3)变换为一般形式, 即

Lr=k(VH)mχn。(4)

式中: k、m、n为常数, 其中k、m应大于0; χ 为影响滑坡运动距离影响的其他因素, 如边坡倾角等。

也有学者提出了更为一般的形式[17, 18, 19, 20, 21], 即

Lr=kVm1Hm2χ1n1…χnnn。(5)

这样既单独考虑了V、H的影响, 同时兼顾考虑了其他多种因素χ i(i=1~n)的影响。

在实际应用中, 具体采用何种形式, 应根据实际情况进行分析, 但应同时保证理论上的正确性和与实际情况的一致性。

2 基于参数相关性分析的滑坡运动距离统计模型

下面首先以李秀珍等[22]提供的“ 5· 12” 汶川地震诱发的滑坡案例(表1)及相应的滑坡几何模型(图1)为例对影响滑坡运动距离的主要因素进行分析, 以评价各因素与滑坡运动距离的相关性, 而后基于式(4)或(5)建立相应的统计模型。

表1 汶川地震触发的46个滑坡概况及运动距离计算结果 Tab.1 Overview of 46 landslides induced by Wenchuan earthquake and their movement distance calculation results

根据第1节的理论分析及前人研究成果[18, 19, 20, 21, 22], 影响滑坡运动距离的因素主要有滑坡体积V、滑坡前后缘高差H、边坡初始倾角θ 等。基于式(4), 这里首先分别单独考虑V、H、VH及θ 的相关性, 如图2。

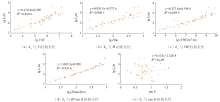图2 滑坡运动距离Lr与各主要因素的相关性Fig.2 Correlation between the landslide movement distance Lr and several major factors

可以看出, lg Lr与lg V、lg H、lg(VH)、lg(H/tan θ )及tan θ 的相关性系数R2分别为0.824 6、0.800 1、0.859 5、0.933 6和0.000 05, 由此可以看出滑坡运动距离与滑坡体积和滑坡前后缘高差的相关性最强, 而与边坡初始倾角的相关性最低。同时相比而言, 其与VH的相关性要比与V和H的单独相关性要强。因此, 根据上述分析, 提出如式(6)的5种统计模型, 然后进行对比分析, 以从中选择相应的最优模型。

Lr=f1(H, V)f2(VH)f3(H, V, tanα)f4(VH, tanα)f5(V, H/tanα)　　。(6)

式中: f1~f5为5个不同的函数, 这里称其对应的模型分别为模型①— ⑤。

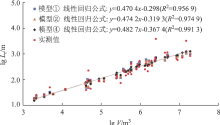
利用多元回归理论, 可得到上述5个模型的统计公式如表2, 可以看出5个模型的相关性均较强, 均在可接受范围内。然而由前述理论分析及大量实测数据统计发现, 滑坡运动距离一般与滑坡体积是成正相关的, 因此尽管模型③、⑤的相关性系数是最高的, 但是随着滑坡体积的增加, 其运动距离反而是减小的, 因此与理论分析不甚符合, 应舍去。下面重点考虑模型①、②和④, 其计算结果如图3和表1所示。可以看出模型④的相关性要略优于其他两个模型, 且由图2(c)可以看出, 滑坡运动距离与VH的相关性也要略优于其与V和H的相关性, 因此认为模型④为最优模型。

表2 滑坡运动距离统计回归模型 Tab.2 Statistical regression model for the landslide movement distance

图3 3种模型计算结果及与实测值对比Fig.3 Comparison between calculation results and test results of three models

3 基于可靠度理论的滑坡运动距离统计模型

然而利用第2节所述方法所得模型④的回归公式, 是基于最小二乘法的最小误差原理, 即由预测值与实际值误差的平方和最小而得到的, 因此由模型④预测得到的滑坡运动距离更趋近于平均值。也就是说实际滑坡运动距离小于或大于预测值的概率均为50%。而当滑坡可能威胁到重要交通设施(如重要公路和铁路)或重点工程(如大型水电站等)和人员时, 上述预测模型的可靠性显然太低了。为此, 这里借鉴王新生等[23]的研究思想, 提出基于可靠度理论的滑坡运动距离统计模型。

由于利用回归方法得到的模型④不是表示滑坡运动距离Lr与滑坡体积V、滑坡前后缘高差H及边坡初始倾角θ 的函数关系, 而是它们之间的相关关系。这是因为由于滑坡本身及场地条件的不确定性和特殊性, 不可能找出一个确定的函数关系式, 而只能是一定超越概率或置信度下的相关关系。因此, 对于任意一个滑坡, 由模型④计算出的Lr0只是Lr的估计值或期望值, 而实际的Lr值往往只是在Lr0附近的区间内, 而该区间的大小也与置信度的选择有关, 置信度越高, 区间就越大, 即Lr是在区间[m1(VH)m2(tan θ )m3, n1(VH)n2(tan θ )n3], 其中: mi、ni(i=1~3)为系数。

为了方便对比和实际应用, 仍以表1所示滑坡为例, 表3给出了4种不同置信度时的滑坡运动距离回归公式。

表3 4种不同置信度时的滑坡运动距离回归公式 Tab.3 Regression formula for the landslide movement distance with four different confidences

由表3可知, 随着置信度的提高, 滑坡运动距离预测的区间范围越来越大。在实际工程中, 如果选择了较高的置信度, 相应地划定的滑坡危险区范围也会随之增加, 进而会增加相应的搬迁或防护工程量及费用。因此, 在实际工程中, 应根据工程的重要程度选择合理的置信度。

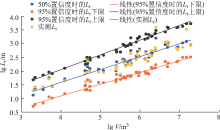
下面以95%的置信度为例进行说明, 统计模型选用模型④, 可求得滑坡水平距离的区间范围为[0.253(VH)0.295(tan θ )-0.776, 1.053(VH)0.372(tan θ )-0.07], 计算结果如图4。

图4 不同置信度时的滑坡运动距离预测结果Fig.4 Predictions of the landsilde movement distance with different confidences

可以看出, 当置信度为50%时, 计算结果与实测结果最为吻合, 二者的线性回归曲线基本一致, 也就是说二者的平均值基本相等。因此可以认为当置信度为50%时, 约有50%的实测结果超过了预测值, 这对于滑坡运动距离范围内有重要设施的情况来说, 是偏于危险的。然而当置信度取为95%时, 实际的滑坡运动距离基本上都落在相应预测值的上、下限范围内, 因此可以达到有效保护重要设施的目的, 但是相应地也提高了滑坡水平运动距离的预测范围, 也随之增加了相应的搬迁和防护费用。

因此, 在实际工程中, 应慎重权衡安全性与经济性的关系, 选择一个合理的置信度, 从而达到安全性与经济性的最佳统一。

4 结论

(1)在前人提出的基于能量守恒原理的滑坡运动距离理论模型基础上, 分析了影响滑坡运动距离的主要影响因素, 认为滑坡运动距离与滑坡体积V和滑坡前后缘高差H成正相关, 并给出了滑坡运动距离与各主要影响因素的一般函数关系式。

(2)基于参数相关性分析, 对影响滑坡运动距离的主要因素进行了研究, 认为滑坡体积V、滑坡前后缘高差H及其组合VH与滑坡运动距离的相关性显著, 且为正相关, 由此采用多元回归法建立了合理的统计模型。

(3)将可靠度理论引入上述统计模型中, 提出了不同置信度时的滑坡运动距离统计模型计算方法, 并给出了回归公式。算例分析表明, 置信度越高, 预测得到的滑坡运动距离区间范围就越大, 相应的搬迁和防护费用就越高。因此, 应根据实际情况, 选择合理的置信度, 以达到经济性和安全性的最佳统一。

(4)研究可为滑坡失稳后致灾范围的预测、评估及受威胁人员和财产的搬迁与防护提供有益指导。但由于研究结论是基于汶川地震诱发的震中附近地区的滑坡而得到的, 因而对由其他形式触发的、其他地区的滑坡, 其适用性仍需进一步研究。

(责任编辑: 刘丹)

参考文献
[1] 黄润秋, 裴向军, 李天斌. 汶川地震触发大光包巨型滑坡基本特征及形成机理分析[J]. 工程地质学报, 2008, 16(6): 730-741.
Huang R Q, Pei X J, Li T B. Basic characteristics and formation mechanism of the largest scale land slide at Daguangbao occurred during the Wenchuan earthquake[J]. Journal of Engineering Geology, 2008, 16(6): 730-741. [本文引用:1]
[2] 樊晓一, 乔建平. “坡”、“场”因素对大型滑坡运动特征的影响[J]. 岩石力学与工程学报, 2010, 29(11): 2337-2347.
Fan X Y, Qiao J P. Influence of land slide and ground factors on large-scale land slide movement[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(11): 2337-2347. [本文引用:1]
[3] Aaron J, Mcdougall S, Nolde N. Two methodologies to calibrate land slide runout models[J]. Land slides, 2019, 16(5): 907-920. [本文引用:1]
[4] Xu Q, Li H J, He Y S, et al. Comparison of data-driven models of loess land slide runout distance estimation[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(2): 1281-1294. [本文引用:1]
[5] Scheidegger A E. On the prediction of the reach and velocity of catastrophic land slides[J]. Rock Mechanics, 1973, 5(4): 231-236. [本文引用:3]
[6] Sassa R. Measurement of the apparent friction angle during rapid loading by the high-speed high stress ring shear apparatus—Interpretation of the relationship between land slide volume and the apparent friction during motion[J]. Land slides, 1992, 1-2: 545-552. [本文引用:1]
[7] 刘红岩, 阎锡东, 张小趁, 等. 滑坡运动距离预测的统计模型及其改进[J]. 灾害学, 2022, 37(4): 6-1017.
Liu H Y, Yan X D, Zhang X C, et al. The statistical model for the movement distance forecast of the land slide and its improve-ment[J]. Journal of Catastrophology, 2022, 37(4): 6-1017. [本文引用:3]
[8] 王家鼎, 张倬元. 地震诱发高速黄土滑坡的机理研究[J]. 岩土工程学报, 1999, 21(6): 670-674.
Wang J D, Zhang Z Y. A study on the mechanism of high-speed loess land slide induced by earthquake[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 670-674. [本文引用:1]
[9] 樊晓一. 岩土体与场地条件作用下的滑坡碎屑流运动机制研究[M]. 北京: 科学出版社, 2017.
Fan X Y. Land slide-Debris Flow Movement Mechanism Under Rock and Soil Mass and Ground Conditions[M]. Beijing: Science Press, 2017. [本文引用:1]
[10] 王鼐, 王兰民, 王谦, 等. 黄土高原地震作用下黄土滑坡滑距预测方法[J]. 地震工程学报, 2016, 38(4): 533-540.
Wang N, Wang L M, Wang Q, et al. Forecasting method for sliding distance of seismic land slides on the Loess Plateau, China[J]. China Earthquake Engineering Journal, 2016, 38(4): 533-540. [本文引用:1]
[11] 常晁瑜, 薄景山, 李孝波, 等. 地震黄土滑坡滑距预测的BP神经网络模型[J]. 地震工程学报, 2020, 42(6): 1609-1614.
Chang C Y, Bo J S, Li X B, et al. A BP neural network model for forecasting sliding distance of seismic loess land slides[J]. China Earthquake Engineering Journal, 2020, 42(6): 1609-1614. [本文引用:1]
[12] Nian T K, Zhang Y J, Wu H, et al. Runout simulation of seismic land slides using discontinuous deformation analysis (DDA) with state-dependent shear strength model[J]. Canadian Geotechnical Journal, 2020, 57(8): 1183-1196. [本文引用:1]
[13] Mao J, Liu X N, Zhang C, et al. Runout prediction and deposit characteristics investigation by the distance potential-based discrete element method: the 2018 Baige land slides, Jinsha River, China[J]. Land slides, 2020, 18(1): 235-249. [本文引用:1]
[14] Liu Z Y, Su L J, Zhang C L, et al. Investigation of the dynamic process of the Xinmo land slide using the discrete element met-hod[J]. Computers and Geotechnics, 2020, 123: 103561. [本文引用:1]
[15] 陈红旗, 徐永强, 庄茂国, 等. 地质灾害应急支撑体系建设基本问题分析[J]. 中国地质灾害与防治学报, 2011, 22(4): 108-111.
Chen H Q, Xu Y Q, Zhuang M G, et al. Study on the construction of geological disaster emergency support system[J]. The Chinese Journal of Geological Hazard and Control, 2011, 22(4): 108-111. [本文引用:1]
[16] 郑光, 许强, 彭双麒. 岩质滑坡-碎屑流的运动距离计算公式研究[J]. 岩土力学, 2019, 40(12): 4897-4906.
Zheng G, Xu Q, Peng S Q. Calculation model of the long-runout distance of rock avalanche[J]. Rock and Soil Mechanics, 2019, 40(12): 4897-4906. [本文引用:1]
[17] 詹威威, 黄润秋, 裴向军, 等. 沟道型滑坡-碎屑流运动距离经验预测模型研究[J]. 工程地质学报, 2017, 25(1): 154-163.
Zhan W W, Huang R Q, Pei X J, et al. Empirical prediction model for movement distance of gully-type rock avalanches[J]. Journal of Engineering Geology, 2017, 25(1): 154-163. [本文引用:1]
[18] 樊晓一, 张睿骁, 胡晓波. 沟谷地形参数对滑坡运动距离的影响研究[J]. 地质力学学报, 2020, 26(1): 106-114.
Fan X Y, Zhang R X, Hu X B. Study on the influence of valley topographic parameter on the moving distance of land slide[J]. Journal of Geomechanics, 2020, 26(1): 106-114. [本文引用:2]
[19] 樊晓一, 胡晓波, 张睿骁, 等. 开阔型地形条件对滑坡运动距离的影响研究[J]. 自然灾害学报, 2018, 27(5): 188-196.
Fan X Y, Hu X B, Zhang R X, et al. Study on the open topography influence on the moving distances of land slides[J]. Journal of Natural Disasters, 2018, 27(5): 188-196. [本文引用:2]
[20] 杨海龙, 裴向军, 樊晓一. 坡脚型滑坡运动特征分析及运动距离预测[J]. 工程地质学报, 2019, 27(6): 1379-1388.
Yang H L, Pei X J, Fan X Y. Movement characteristics and distance prediction of slope toe land slides[J]. Journal of Engineering Geology, 2019, 27(6): 1379-1388. [本文引用:2]
[21] 樊晓一, 冷晓玉, 段晓冬. 坡脚型与偏转型地震滑坡运动距离及地形因素作用[J]. 岩土力学, 2015, 36(5): 1380-1388.
Fan X Y, Leng X Y, Duan X D. Influence of topographical factors on movement distances of toe-type and turning-type land slides triggered by earthquake[J]. Rock and Soil Mechanics, 2015, 36(5): 1380-1388. [本文引用:2]
[22] 李秀珍, 孔纪名. “5·12”汶川地震诱发滑坡的滑动距离预测[J]. 四川大学学报(工程科学版), 2010, 42(5): 243-249.
Li X Z, Kong J M. Runout distance estimation of land slides triggered by “5·12” Wenchuan earthquake[J]. Journal of Sichuan University (Engineering Science Edition), 2010, 42(5): 243-249. [本文引用:2]
[23] 王新生, 刘红岩. 爆破振动速度回归分析中 K值的合理选用[J]. 武汉理工大学学报, 2005, 27(11): 103-105, 109
Wang X S, Liu H Y. Reasonable selection of k in blasting vibration velocity regression analysis and its application[J]. Journal of Wuhan University of Technology, 2005, 27(11): 103-105, 109 [本文引用:1]