第一作者简介: 朱涛(1984—),男,工程师,主要从事地质灾害危险性评估、地质灾害治理施工、山水林田湖草生态修复、地质测绘等领域的工作。Email: zhut1232022@163.com。
为准确掌握浅层顺层滑坡的成因机制,合理评价其稳定性,基于滑坡所处地质条件,先开展其成因机制分析,再利用传递系数法和变形预测模型分别开展滑坡稳定性的现状评价及预测评价。实例分析表明: 浅层顺层滑坡的影响因素相对较多,且由于浅层滑坡的滑体厚度较薄,受外界扰动影响易较大,因此,浅层滑坡对各类因素的敏感性均较强。在滑坡稳定性现状评价结果中: 天然工况条件下的稳定性系数为1.21,属稳定状态; 暴雨工况条件下的稳定性系数为1.02,属欠稳定状态; 地震工况条件下的稳定性系数为1.09,属基本稳定状态。在滑坡稳定性预测评价结果中,滑坡各监测点位置处的变形预测速率均一定程度上大于现有变形速率,说明滑坡后续累计变形仍会进一步加速,其说明在本次监测时段后的滑坡稳定性将趋于减弱,需尽快开展此滑坡防治研究。研究成果可为浅层顺层滑坡灾害防治提供一定的理论指导。
In order to accurately grasp the formation mechanism of shallow bedding landslides and reasonably evaluate their stability, the authors in this article first conduct an analysis of their formation mechanism based on the geological conditions of the landslide, and then use the transfer coefficient method and deformation prediction model to carry out the current situation evaluation and prediction evaluation of landslide stability. Example analysis showed that there were relatively many influencing factors for shallow bedding landslide, and they were easily affected by external disturbances due to the thin thickness of the sliding body of shallow landslide. Therefore, shallow bedding landslide was highly sensitive to various factors. In the evaluation results of landslide stability status quo, the stability coefficient under natural condition was 1.21, with stable status, the stability coefficient under rainstorm condition was 1.02, with unstable status. and the stability coefficient under earthquake condition was 1.09, with basically stable status. In the landslide stability prediction and evaluation results, the deformation prediction rates at each monitoring point of the landslide were higher than the existing deformation rates to some extent, indicating that the cumulative deformation of the landslide would continue to accelerate in the future. The results also indicate that the landslide stability tend to weaken after this monitoring period, and it is necessary to carry out landslide prevention and control research as soon as possible. The study results could provide certain theoretical guidance for the prevention and control of shallow bedding landslide disaster.
浅层顺层滑坡在我国广泛分布。按《GB/T 32864—2016滑坡防治工程勘查规范》[1]规定, 浅层滑坡定义为滑体厚度小于10 m。此类滑坡规模一般较小, 但其自稳能力相对也较弱, 易出现局部变形破坏, 若区内居民较多, 其潜在危害显著, 且该类滑坡易引发水土流失, 不利于环境保护。因此, 该文将浅层顺层滑坡作为研究对象, 重点开展其成灾机制分析及稳定性评价[2, 3]。目前, 许多学者利用数值模拟、数理统计等手段, 从浅层滑坡影响因素出发, 研究了降雨、植被等对浅层滑坡稳定性的影响规律, 并探究了此类滑坡的演化机制[4, 5, 6, 7]。
上述研究表明: 一方面, 开展浅层滑坡研究具有重要意义, 即其能为此类滑坡灾害防治提供具有针对性的理论基础; 另一方面, 浅层滑坡发育存在一定的区域性特征, 即不同地区的浅层滑坡具有相应差异。因此, 仍有必要针对具体实例开展进一步研究。浅层滑坡影响因素与一般滑坡的影响因素相对较为一致, 但也具一定的特征性。因此, 本文提出基于浅层滑坡所处地质条件, 开展其成因机制分析。同时, 以往滑坡稳定性评价多侧重于现状评价, 缺乏稳定性预测评价, 分析结果的全面性受限, 因此, 本文提出将滑坡稳定性评价过程划分为两步, 即稳定性现状评价和预测评价, 并通过传递系数法实现其稳定性现状评价, 再通过变形预测实现其稳定性预测评价。研究旨在有效掌握浅层顺层滑坡的成灾机制, 并为其稳定性评价提供一种思路, 从而奠定灾害防治的理论基础。
据工程实际, 滑坡常用的现状稳定评价模型主要是传递系数法, 其原理已在《GB/T 32864—2016滑坡防治工程勘查规范》[1]中详述, 因此, 不再赘述[8, 9]。
(1)计算工况。在滑坡稳定性现状评价过程中, 共设置了3种工况: 工况1, 天然工况, 该工况是评价滑坡天然状态下的稳定性; 工况2, 暴雨工况, 该工况是评价滑坡暴雨状态下的稳定性; 工况3, 地震工况, 该工况是评价滑坡地震状态下的稳定性。
(2)计算参数。据滑坡勘查成果, 其稳定性计算参数见表1。
| 表1 不同工况条件计算参数 Tab.1 Calculation parameters under different conditions |
(3)稳定性状态划分。据《GB/T 32864—2016滑坡防治工程勘查规范》[1], 以稳定性系数Fs为基础, 开展滑坡稳定性状态划分。若Fs属小于0时, 滑坡处于不稳定状态; 若Fs属[0, 1.05)区间时, 滑坡处于欠稳定状态; 若Fs属[1.05, 1.15)区间时, 滑坡处于基本稳定状态; 若Fs属大于等于 1.15 时, 滑坡处于稳定状态。
一般来说, 滑坡变形越大, 其稳定性相对应越弱, 因此, 提出利用变形预测来开展滑坡稳定性预测评价。灰色模型(简称GM(1, 1)模型)能在部分信息未知情况下实现非线性预测, 使得其在变形预测领域取得了广泛应用, 提出利用其构建滑坡变形预测模型, 但传统GM(1, 1)模型多具离散形式, 而滑坡变形具有连续形式。为解决该问题, 袁德宝等[10]将分数阶算子引入其中, 构建出了分数阶算子条件下的灰色模型(简称EGM(1, 1)模型), 且考虑到分数阶算子是由使用者确定, 为保证其最优性, 提出利用改进粒子群算法(improve particle swarm optimization, IPSO)[11]开展其优化处理。该方法是粒子群算法的改进型, 结合其基本原理, 其寻优过程有4步。
(1)开展粒子种群的初始信息设置, 如将学习因子设定为1和2, 权重因子设定为0.7, 种群规模设定为600。
(2)将各粒子的当前位置设置为分数阶算子, 并以其预测结果的平均绝对百分误差为基础, 初步确定出群体的最佳粒子位置。
(3)更新每个粒子的位置和速度, 并重新计算每个粒子更新后的平均绝对百分误差值, 将其与最佳粒子的平均绝对百分误差值对比, 若前者更优, 则将最佳粒子位置进行重新设置, 反之, 保留原位置。
(4)当完成寻优后, 将全局最佳粒子对应的分数阶算子输出, 即可完成其寻优过程。
虽然利用IPSO算法保证了EGM(1, 1)模型分数阶算子的最优性, 但限于滑坡变形的非线性特征, 其预测结果还是会存在一定误差, 即IPSO-EGM(1, 1)模型的预测结果仍会存在预测误差。为充分保证预测精度, 再提出利用混沌理论开展其误差弱化处理[12, 13]。结合其基本原理, 将其预测步骤说明如下。
先利用Lyapunov指数法开展待预测误差序列的混沌特征识别, 按照其识别流程, 计算判别参数λ , 其计算公式为
式中: tM、t0为时间变量, s; M为迭代次数, 次; Li为原始距离值; li为重构后的距离值。
以λ 值开展误差序列的混沌特征识别, 即: 若λ max值大于0, 那么预测误差序列具混沌特征; 反之, 则不具混沌特性。
利用延迟时间算法确定嵌入维数, 并利用去偏复自相关法确定延迟时间, 通过此两参数可实现误差序列的相空间重构。同时, 再利用Lyapunov指数法开展误差序列的预测处理, 具体过程为: 将ψ i作为预测中心, 计算与其最近相邻点间的距离d。公式为
式中: ψ i、ψ j为相空间节点。
若d值最小, 即可反推出预测误差的预测值。
据上, 最终将滑坡变形预测模型确定为IPSO-EGM(1, 1)-WT模型。
基于预测结果, 先引入两个速率统计量, 即V1速率(mm/周)和V2速率(mm/周), 前者是实测数据最后4期的变形速率均值, 后者是4期外推预测结果的变形速率均值。若V1速率相对更大, 说明滑坡变形趋于收敛, 其后续稳定性亦趋于稳定; 反之, 说明滑坡变形趋于继续增加, 其后续稳定性亦趋于不稳定。
某滑坡位于斜坡前缘地段, 平面具扇形形态(图1), 所处斜坡坡度为20° ~40° , 植被较发育。据现场调查, 滑坡主滑方向为30° , 纵向长约 150 m, 宽度间于90~180 m。土层厚度具有一定差异, 主要间于3.2~6.1 m, 平均厚度约4.5 m, 总体积约8.4× 104 m3, 属典型的浅层滑坡。
据钻探成果, 将滑坡结构地层特性阐述如下。
(1)滑体土。岩性主要是填土和粉质黏土: 前者主要分布于滑坡中上部, 仅局部分布, 对滑坡影响有限; 后者在滑坡区广泛分布, 紫红色, 多呈可塑-硬塑状, 局部含有少了角砾, 母岩成分多是泥岩, 磨圆度较差。
(2)滑带。岩性主要是黏土, 紫红色, 属泥岩风化后的产物, 整体力学性质较差, 遇水易软化, 多呈可塑状。
(3)滑床。岩性为泥岩, 紫红色, 节理裂隙较发育, 岩体整体完整性相对较差, 强度中等, 岩层产状为46° ∠34° , 结合滑坡主滑方向, 该滑坡具有顺层滑坡特征。
将主滑面(即图1中A-A'剖面)的地层结构阐述如图2所示。
该滑坡早在2010年雨季就开始出现变形情况, 其后每年变形均有所发育, 主要表现为局部房屋倒塌及裂缝发育, 其中, 裂缝多会后期自动愈合。据上, 该滑坡变形特征显著, 且区内威胁居民相对较多, 因此, 开展本研究十分必要。
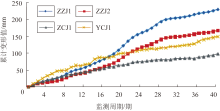
为定量掌握滑坡变形量, 在滑坡上共计布置了4个监测点, 用于开展监测位置的总位移监测, 其中, 主轴上布置了2个, 左右两侧分别布置1个, 具体位置见图1。据统计, 共计得到40期(监测周期为2 d, 监测时段为2022年7月8日至2022年9月26)的滑坡变形数据, 其变化曲线如图3所示。
据图3, 滑坡各位置处的累计变形总体呈持续增加趋势, 只是局部短时存在负增长。ZZJ1监测点的累计变形量为229.03 mm, 相对最大, 说明后缘相对更不稳定; ZZJ2监测点的累计变形量为166.98 mm; 两者均位于滑坡主轴上, 充分说明主轴是滑坡稳定性相对最弱位置, 侧面也验证了后续通过主轴开展滑坡稳定性现状评价的可行性。在滑坡两侧, 西北侧ZCJ1监测点的累计变形量为97.63 mm, 东北侧YCJ1监测点的累计变形量为148.33 mm, 对比而言, 滑坡右侧变形相对更大。
2.2.1 滑坡影响因素分析
一般来说, 浅层滑坡变形影响因素相对较多, 其主要可从物源条件、地形条件及水源条件等方面开展分析, 具体分析如下。
(1)土层厚度因素。土层较薄是浅层滑坡的特有特征。一方面, 土层薄, 利于降雨软化, 促使滑坡易出现变形破坏, 且该类变形无统一规律性; 另一方面, 土层厚度对滑坡破坏形式具有一定影响, 若土层相对较薄, 更易出现滑移破坏, 若土层相对较厚, 更易出现蠕滑破坏。
(2)地形条件因素。地形条件对浅层滑坡的影响较大, 又可进一步细分为坡度因素、地形因素及高差因素。①坡度因素。坡度是滑坡灾害的重要成因, 一般来说, 斜坡坡度越陡, 其越容易发生失稳破坏。结合调查成果, 在坡度间于20° ~40° 时, 浅层滑坡更易发育。②地形因素。地形对浅层滑坡的影响规律主要表现为: 地形为凸形时, 浅层滑坡相对最易发育; 地形为直线形时, 浅层滑坡发育一般; 地形为凹形时, 浅层滑坡一般不发育。③高差因素。由于浅层滑坡滑体厚度较薄, 其固有稳定属性相对就较差, 因此, 该类滑坡难以形成较大的高差。滑坡发育的主要高差范围是20~50 m, 其次是50~100 m, 其余高差范围的滑坡发育相对较少。
(3)地层岩性因素。地层岩性与浅层滑坡的形成具有密切关系, 一般来说, 浅层滑坡发育区的地层力学参数均较低, 即软质岩更易形成浅层滑坡, 其次是软硬相间岩, 而硬质岩不易形成浅层滑坡。
(4)地质构造因素。一方面, 地质构造是形成滑坡区的原始地形地貌, 是浅层滑坡形成的基础; 另一方面, 地质构造会极大程度上影响滑坡地层的完整性, 对区内节理系统的发育也有一定的影响, 进而影响滑坡稳定性。
(5)植被与土地利用因素。该因素主要包含植被覆盖因素和土地利用类型因素。①植被覆盖因素。一般来说, 植被对土体具有一定的加固作用, 主要表现为: 植物根系深入土层中, 一定程度上抑制了土体裂隙的发育, 可有效减少坡面破坏。由于浅层滑坡滑体厚度本身较薄, 此因素对其影响显著, 从植被极疏至中等再至茂密, 浅层滑坡的发育频率越来越少, 尤其在植被茂密时, 几乎无浅层滑坡发育。②土地利用类型因素。由于土地利用类型不同, 其对应植被覆盖情况及其种类均随之不同, 这也会一定程度上影响土体对雨水的吸收情况。据调查, 旱地、灌木类型具较高浅层滑坡发育率, 其余类型的发育率相对较低。
(6)降雨因素。降雨一直以来就是滑坡失稳破坏的重要诱因, 其对浅层滑坡尤为明显, 主要是因为浅层滑坡滑体较薄, 雨水入渗路径较短, 即使小雨也可能造成局部失稳, 其影响规律可总结为: 一方面, 雨水入渗不仅会增加滑体重度, 还会减弱滑面抗剪强度, 降低滑坡稳定性; 另一方面, 若存在短时强降雨, 易在地表形成径流, 造成坡面冲刷等, 这对浅层滑坡稳定极为不利。
(7)人类工程活动因素。一般来说, 存在滑坡灾害的范围均会具有一定程度的人类工程活动, 其对滑坡的影响主要表现为: 工程活动造成削坡、减载等, 打破了原有坡体的内力平衡, 诱使滑坡灾害发生, 尤其对于浅层滑坡, 轻微的扰动极可能诱发局部变形。
据上, 浅层滑坡的影响因素相对较多, 且其对各类因素的敏感性均较强, 这是因为其滑体厚度较薄, 受外界扰动影响较大。
2.2.2 滑坡形成机制分析
结合上述滑坡影响因素分析及工程实例概况, 将该文实例滑坡的形成机制总结如下。
(1)滑坡所处斜坡坡度为20~40° , 且具顺向坡的坡体结构, 为滑坡灾害形成奠定了基础。
(2)滑坡区基岩为泥岩, 本身遇水易软化, 易形成软弱潜在滑面, 其形成机理为: 滑体较薄, 雨水易入渗, 且当渗至基覆界面时, 下覆泥岩又具一定隔水性, 进而雨水在基覆界面汇集; 同时, 降雨停止后, 基覆界面处的水分蒸发也是相对最晚蒸发, 如此长期作用, 就会形成基覆滑面。
在各类影响因素综合作用影响下, 尤其是在降雨、人类工程活动长期诱发作用条件下, 滑坡易出现局部变形, 存在整体失稳风险。
2.3.1 稳定性现状评价
据1.1节思路, 通过传递系数法开展滑坡主滑面(即A-A'剖面)的稳定性分析, 其计算结果如表2所示。工况1属稳定状态; 工况2属欠稳定状态; 工况3属基本稳定状态。通过上述, 在稳定性现状条件下, 得出该滑坡在天然状态下仍处于稳定状态, 但在不利工况条件下, 存在失稳风险。
| 表2 A-A'剖面稳定性计算结果 Tab.2 Stability calculation results of A-A' profile |
2.3.2 稳定性预测评价
该节重点按照1.2节思路, 通过IPSO-EGM(1, 1)-WT模型开展滑坡稳定性预测评价。在该过程中, 将前35期数据作为训练集, 后5期数据作为验证集, 且考虑到IPSO-EGM(1, 1)-WT模型具有递进优化组合流程, 提出以ZZJ1监测点为例, 进行对比分析, 以验证各递进优化组合步骤的有效性。
为便于后续描述, 将各递进优化组合步骤的预测模型命名如下。预测模型1: GM(1, 1)模型; 预测模型2: EGM(1, 1)模型; 预测模型3: PSO-EGM(1, 1)模型; 预测模型4: IPSO-EGM(1, 1)模型; 预测模型5: IPSO-EGM(1, 1)-WT模型。
首先, 得到5类预测模型的预测结果如表3所示。
| 表3 预测模型1—5的预测结果统计 Tab.3 Prediction results of prediction model 1—5 |
据表3, 以各预测模型的相对误差为评价指标, 统计其特征参数如下。预测模型1的相对误差平均值为3.17%, 方差值为0.014 0(%)2; 预测模型2的相对误差平均值为2.96%, 方差值为0.008 8(%)2; 预测模型3的相对误差平均值为2.57%, 方差值为0.005 7(%)2; 预测模型4的相对误差平均值为2.32%, 方差值为0.004 9(%)2; 预测模型5的相对误差平均值为2.02%, 方差值为0.003 6(%)2。
由此可知, 从预测模型1至模型5, 预测精度及预测结果的稳定性具逐步提高趋势, 充分验证了各递进优化组合步骤的有效性。其中, 预测模型1和预测模型2对比, 验证了分数阶算子对灰色模型的优化能力; 预测模型3和预测模型4对比, 得出IPSO算法较粒子群(partide swarm optimization, PSO)算法具有更好的优化能力; 预测模型5较其余模型的预测效果优势明显, 充分验证了通过IPSO-EGM(1, 1)-WT模型开展滑坡变形预测的合理性。
其次, 再以IPSO-EGM(1, 1)-WT模型开展其余监测点的预测分析, 结果如表4所示。
| 表4 各监测点的最终预测结果 Tab.4 Final prediction results for each monitoring point |
据表4, 各监测点的预测结果存在一定差异, 其预测结果的特征参数为如下。ZZJ1监测点的相对误差平均值为2.02%, 方差值为0.003 6(%)2; ZZJ2监测点的相对误差平均值为2.04%, 方差值为0.004 3(%)2; ZCJ1监测点的相对误差平均值为2.11%, 方差值为0.006 5(%)2; YCJ1监测点的相对误差平均值为1.97%, 方差值为0.002 2(%)2。
据上, 各监测点的相对误差均值多在2%左右, 方差值也较小, 充分验证了IPSO-EGM(1, 1)-WT模型的预测能力及稳定性。
最后, 再统计得到各监测点的V1速率和V2速率如图4所示。
据图4, 各监测点的V2速率均不同程度地略大于V1速率, 因此, 说明滑坡各位置处的后续变形速率还会进一步增加, 滑坡累计变形具加速增加趋势, 即滑坡稳定性在现有基础上, 还会进一步减弱。
综合2.2.1节滑坡稳定性现状评价结果和 2.2.2 节滑坡稳定性预测评价结果, 得出本文实例滑坡现有稳定性已较弱, 剩余安全储备已较少, 且后续变形仍会加速, 不利于滑坡稳定, 即其后续稳定性仍会进一步减弱, 需尽快开展此滑坡防治研究。
(1)浅层滑坡的影响因素主要包括土层厚度因素、地形条件因素、地层岩性因素、地质构造因素、植被与土地利用因素、降雨因素及人类工程活动因素, 尤其是在地形、坡体结构等因素存在的基础上, 受降雨、人类工程活动长期诱发产生的。
(2)在滑坡稳定性现状评价结果中: 天然工况条件下, 稳定性系数为1.21, 属稳定状态; 暴雨工况条件下, 稳定性系数为1.02, 属欠稳定状态; 地震工况条件下, 稳定性系数为1.09, 属基本稳定状态。说明不利工况条件下具潜在失稳风险。在后续预测过程中, IPSO-EGM(1, 1)-WT模型能有效实现浅层滑坡的高精度预测, 且预测结果显示, 滑坡各位置处的后续变形速率还会进一步增加, 且滑坡累计变形具加速增加趋势, 说明在本次监测时段后的滑坡稳定性将趋于减弱。
(责任编辑: 刘丹)
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|