大地电磁测深数据处理方法技术进展

引用本文

张昆, 刘磊, 马兴知, 杨雨凡. 大地电磁测深数据处理方法技术进展[J].中国地质调查, 2024,11(5): 129-138.
ZHANG Kun, LIU Lei, MA Xingzhi, YANG Yufan. Technical progress of processing methods for magnetotelluric sounding data[J].Geological Survey of China, 2024,11(5): 129-138. 复制到剪切板

doi: 10.19388/j.zgdzdc.2024.119

Permissions

《中国地质调查》编辑部所有

大地电磁测深数据处理方法技术进展

张昆^1,^2,^3,⁴, 刘磊^5,^*, 马兴知^1,², 杨雨凡^1,²

1.中国地质科学院,北京 100037

2.自然资源部深地科学与探测技术实验室,北京 100037

3.东华理工大学,江西南昌 330013

4.自然资源部地球物理电磁探测技术重点实验室,河北廊坊 065000

5.湖北省地质局地球物理勘探大队,湖北武汉 430056

通信作者简介: 刘磊(1985—),男,高级工程师,主要从事深部找矿和勘查工作。Email: 23632956@qq.com。

第一作者简介: 张昆(1983—),男,研究员,主要从事深部找矿和探测技术研究工作。Email: zhangkun1010@163.com。

收稿日期: 2024-01-22 修回日期: 2024-09-09

基金资助: 中国地质调查局“华南地区大地电磁应用示范(编号: DD20230231)”、国家自然科学基金“下扬子及邻区岩石圈三维电性结构研究(编号: 42174087)”、自然资源部地球物理电磁法探测技术重点实验室“针对铜镍矿预测的多元电测深数据机器学习技术集成实验(编号: KLGEPT202203)”与自然资源部“全数据智能矿产勘查预测战略研究与技术探索(编号: 121106000000180039-2211)”项目联合资助

摘要

大地电磁测深法以其探测深度大、不受高阻层屏蔽、设备轻便、成本低等优势,被广泛用于地球动力学、成矿系统等研究以及深部资源和(清洁)能源探测、灾害调查等领域。然而,该方法在观测天然电磁场信号方面信号较弱,容易受到噪声干扰,一般需长时间观测和多次叠加方式来获取电性信息,且需同时开展相应的数据处理和分析,以获得更为可靠的地下电性结构。其中,数据处理一般包括时频转换、去噪、阻抗张量和倾子矢量估计,数据分析主要包括电性主轴和介质维度分析。基于前人关于大地电磁测深探测方法的研究成果,针对探测体系中处理、分析的关键环节,总结目前普遍使用的方法,并基于数据处理中的去噪、数据分析中的阻抗和相位张量,介绍探测体系中重要环节的前沿研究方向和成果,分析现有方法各自的特点和优点及其在不同环境和背景下大地电磁场观测数据的适用性,为大地电磁测深的有效、高效应用提供理论信息和基础保障。

关键词: 大地电磁测深; 数据处理; 数据分析; 方法技术

中图分类号:P631.325 文献标志码:A 文章编号:2095-8706(2024)05-0129-10

Technical progress of processing methods for magnetotelluric sounding data

ZHANG Kun^1,^2,^3,⁴, LIU Lei⁵, MA Xingzhi^1,², YANG Yufan^1,²

1. Chinese Academy of Geological Sciences,Beijing 100037,China

2. Laboratory of Deep Earth Sciences and Technology of Ministry of Natural Resources, Beijing 100037, China

3. East China Institute of Technology, Jiangxi Nanchang, 330013, China

4. Key Laboratory of Geophysical Electromagnetic Probing Technologies of Ministry of Natural Resources, Hebei Langfang 065000, China

5. Geophysical Exploration Brigade of Hubei Geological Bureau, Hubei Wuhan 430056, China

Abstract

The magnetotelluric sounding method is widely used in researches on geodynamics, metallogenic system, deep exploration of mineral resource and clean/oil energy and investigation of geological disaster, due to its advantages of large detection depth, penetrating high resistance layers, portable performance and low cost. However, the performance of this method is weak in natural electromagnetic field signals observation, which is easily interfered by noise. The effective electrical information is obtained by long-term observation and multiple superposition, and the related data processing and analysis methods were used to obtain reliable geo-electrical results. Data processing usually includes time-frequency conversion, denoising, estimation of impedance tensor and tipper vector, and data analysis includes electrical strike direction and medium dimension analysis. In this paper, the authors summarized the widely used processing methods for magnetotelluric sounding data, based on previous research and introduced the forefront research directions and achievements focusing on denoising in data processing and impedance and phase tensor in data analysis. The characteristics and advantages of the existing methods, and the applicability to geomagnetic field observation data under different environments and backgrounds were analyzed to provide theorical information and basic guarantee for effective and efficient application of magnetotelluric sounding.

Keyword: magnetotelluric sounding; data processing; data analysis; method and technique

图片选项

0 引言

大地电磁测深(magnetotelluric sounding, MT)方法于20世纪50年代初由前苏联学者Tikhonov^[1]和法国学者Cagniard^[2]提出, 该方法基于超宽频率范围(10 000~0.000 1 Hz)的天然电磁场信号揭示地下不同深度尺度(地壳浅表至上百千米)的电性结构, 以天然场源能量大、频带宽、勘探深度大、仪器设备轻便、不受高阻屏蔽、对低阻分辨率高等优势受到地球物理学家的关注, 主要被用于矿产-地下水-地热资源勘查、油气普查、灾害调查、地壳及岩石圈深部结构研究等领域, 是不可或缺的地球物理深探测方法之一^[3]。其中, 深部结构研究和深部找矿等领域近年来取得了一系列优秀应用成果, 例如: Zhang等^{[4, 5, 6]}利用大地电磁测深剖面结果揭示了华南地区岩石圈电性结构, 发现了陆内俯冲板片痕迹, 并提出了对板片断裂控制成矿系统的新认识; Zhang等^{[5, 7, 8]}利用大地电磁测深三维反演结果揭示胶东和长江中下游典型矿集区地壳精细结构, 并提出对成矿背景和过程的新认识; 赵凌强等^[9]使用5条完全覆盖贺兰山— 银川盆地不同区段的大地电磁剖面数据, 获得了全区域的地壳上地幔尺度精细三维电性结构信息, 推测贺兰山— 银川盆地系统是在区域拉张作用下形成的活动构造带; 薛国强等^[10]利用测大地电磁全阻抗张量数据给出了羊八井地热田三维电性结构模型在不同深度的水平切片和在不同测线的剖面图, 发现羊八井地热田的深部热源。

然而, 天然电磁场极化方向随时间随机变化, 场强相对较弱, 加之地表日益复杂的电磁干扰, 严重影响了大地电磁测深方法的观测质量, 需开展针对不同信号影响因素的数据处理和分析, 为数据解释和地质解译提供可靠信息。本文通过分析各重要环节的前沿研究方向和成果, 为大地电磁测深的有效、高效应用提供理论信息和基础保障。

1 大地电磁测深方法基本原理

大地电磁测深方法通过观测天然场源或远区人工场源的平面二分量电场以及空间三分量磁场分量信号, 获得地下电阻抗和倾子信息^{[11, 12]}。

设时谐因子为exp(-iω t), 频率域中的地电感应电磁场满足下列麦克斯韦微分方程组

$\begin{array}{l} Δ \times E = - χH, \\ Δ \times H = λE, \\ Δ \cdot J = 0, \\ Δ \cdot χH = 0 。 \end{array}$ (1)

式中: Δ × 是旋度算符; Δ · 是散度算符; E为电场强度, V/m; H为磁场强度, T; J为电流密度, A/m²。

χ 与λ 定义为

$\begin{array}{l} χ = - iωμ, \\ λ = σ - iωε, \\ i = \sqrt[]{- 1}, \\ ω = 2 π f (角频率) 。 \end{array}$ (2)

式中: f为频率, Hz; μ 为磁导率, H/m; ε 为介电常数, F/m; σ =1/ρ 为电导率, S/m; ρ 为电阻率, Ω · m。在大地电磁测深应用领域中, 忽略地下介质与空气和真空的磁导率, 以及介电常数之间的微弱差异, 使用空气磁导率(μ ₀)和真空介电常数(ε ₀)近似代替地下半空间介质参数^[13], 而且由于电磁波的使用频率通常相对较低, 因此忽略位移电流 (-iω ε ), 将电磁场表示为

$\begin{array}{l} Δ^{2} E + i μ_{0} σωE = 0, \\ H + Δ H / (iμω) = 0 。 \end{array}$ (3)

式中: Δ 是点积。可以通过求解上述亥姆霍兹方程, 获得地表电场和磁场强度E和H。

假设空气的电导率为0, 地下沿地表侧面的法向电场强度为0(空气侧面的法向电场强度很难稳定的观察到)。MT通常只观测电场强度E和磁场强度H的水平分量以及磁场强度H的法向分量。由于MT的场源来自电离层, 与地面的距离足够远, 因此认为电磁波为垂直入射地表的平面波。根据平面波场入射理论, 可以建立电阻抗(Z)与电场强度水平分量(E_x)和磁场强度水平分量(H_x)的关系表达式^{[13, 14, 15]}以及倾子矢量(T)和磁场强度(H)三分量的关系表达式^{[16, 17]}:

$[\begin{array}{l} E_{x} \\ E_{y} \end{array}] = (\begin{array}{l} Z_{xx} & Z_{xy} \\ Z_{yx} & Z_{yy} \end{array}) [\begin{array}{l} H_{x} \\ H_{y} \end{array}],$ (4)

$\begin{array}{l} H_{z} = [T_{x} T_{y}] [\frac{H_{x}}{H_{y}}] = T_{x} H_{x} + T_{y} H_{y} 。 \end{array}$ (5)

式中: Z为阻抗张量, T为倾子矢量。通过Z, 可以得到更直观的电性参数视电阻率(ρ )和阻抗相位(ϕ )^[2]

$\begin{array}{l} ρ_{ij} = \frac{1}{μω}| Z_{ij} |^{2}, \\ ϕ_{ij} = atan (Imag (Z_{ij}) / Real (Z_{ij})), \\ i = x, y; j = x, y 。 \end{array}$ (6)

式中: atan是正弦计算, Imag是复数虚部; Real是复数实部。

因为电磁波的趋肤效应, 低频信号的穿透深度更大。因此, 不同频率的数据反应不同深度的电性信息, 实现单测点垂向测深。电磁场(E和H)在大地中传播时, 振幅衰减到初始值1/e时的深度定义为穿透深度或趋肤深度, 公式为

$δ = \sqrt[]{\frac{ρ}{π μf}} 。$ (7)

式中: δ 为趋肤深度, 无量纲。

2 大地电磁测深数据采集和处理分析

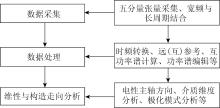
大地电磁测深方法基于采集的时间序列信号, 通过数据处理和分析获得有效电性信息。数据处理步骤主要包括时间序列的频率域转换、远(互)参考处理、互功率谱(电阻抗)计算、功率谱编辑(单频统计数据筛选)等; 数据分析主要包括电性主轴方向、介质维度分析、极化模式分析等^[10](图1)。

	Figure Option View Download New Window
	图1 数据处理分析流程^[10]Fig.1 Data processing and analysis flow^[10]

2.1 数据采集

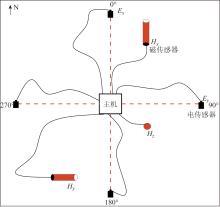
由于地表大地电磁场信号较弱, MT数据质量依赖于测点周围的环境, 野外选点是保证数据质量的第一步, 也是很重要的一步。因此, 测点需远离地表障碍物、干扰源以及地形等影响^[18]。数据采集一般使用“ +” 字型布站方式(图2), 地形或环境影响较大时, 可以采用“ T” 型(单电偶极不对称)或“ L” 型(双电偶极不对称)布站方式。

	Figure Option View Download New Window
	图2 数据采集推荐方式Fig.2 Recommended data collection methods

2.2 数据处理方法

MT数据处理主要指由采集的时间序列计算得到频率域的功率谱矩阵和传递函数的过程(阻抗张量、倾子矢量等)^{[13, 19, 20]}, 普遍应用流程为时频转换— 去噪— 传递函数计算。时频转换一般采用快速傅立叶变换, 需要选择时窗长度、分频策略以及中心频点, 得到不同时间段的功率谱矩阵, 通过功率谱矩阵叠加方式获得每个频点的稳定数据^{[21, 22, 23]}。为了消除或降低误差, 一般采用最小二乘估计法获得最优统计结果^{[13, 24, 25, 26]}。然而, 由于天然电磁场信号弱、频带宽, 该方法在工业发达地区受电磁噪声干扰较为严重, 难以估算准确的阻抗张量和倾子矢量。去除大地电磁信号中的强噪声干扰, 获得无偏的阻抗估计是后续数据处理解释的基础。远参考法利用远区洁净测站磁场信号数据与实测数据卷积, 减弱或消除磁场不相关噪声, 获得高质量阻抗张量^[27]。该方法仍然会产生一定的统计误差, 并且不能消除相关噪声的影响^[26]。Robust方法^[24]针对相关信号和不相关噪声, 根据观测误差和剩余功率谱的大小对数据进行加权处理, 降低强噪声干扰数据的权重, 能够压制非高斯分布噪声, 较最小二乘估计法有一定优势, 但不能解决近场等相关噪声问题。Robust方法和远参考方法通常结合应用, 但很难解决磁场和电场时间序列均受相关噪声干扰的问题。此外, 前人还提出了连续小波变换^{[28, 29]}、数学形态滤波^[30]、多参考站数据噪声统计^[31]、基于远参考磁场数据的磁场信号分离方法^[32]等, 本文主要介绍数据处理的基本原理和新方法进展。

2.2.1 时频转换

信号由时间域到频率域的转换方法最初采用快速傅里叶变换, 后来逐渐发展出小波变换和广义S变换等方法。

(1)快速傅里叶变换。快速傅里叶变换是一种时频转换方法, 将时间序列转换为频域信号。时间序列(x(t))基于窗函数(g(t)), 通过快速傅里叶变换转换为频率域电磁场数据(x(f)), 公式为

$x (f) = \int_{-}^{P} g (t) x (t) e^{- i 2 π ft} d t 。$ (8)

式中: t为时间, s; f为频率, Hz; P为采样范围, s。

(2)小波变换。傅里叶变换是分析时间序列的传统工具, 是一种全局性的变换, 只适用于处理线性系统的平稳信号, 只能检测出信号的主要频率以及两个信号间的相位差, 具有一定的局限性, 无法检测主要频率变化以及短周期相位变化。而小波变换是一种时频分析方法, 是一种自适应的时域和频域同时局部化方法, 能够调节时频窗大小, 分析低频或者高频的局部信号^[16]。

定义信号S的连续小波变换为

$W_{g} S (t, a) = \int_{-}^{\infty} \frac{1}{a} g (\frac{τ - t}{a}) \cdot S (τ) d τ 。$ (9)

式中: a为尺度因子; g_t_,_a(τ )= $\frac{1}{a}$ g $(\frac{τ - t}{a})$ 为小波系类; t为位移因子; τ 是位移因子积分量, g(t)为母小波。

常用的小波函数包括Morle小波、Cauchy小波等, 其中Morle小波表示为

$\begin{array}{l} g (t) = e^{2 π it} e^{- \frac{t^{2}}{(2 σ^{2})}}, \\ \hat{g} (ω) = σ \sqrt[]{2 π} e^{- σ^{2} (ω - \frac{2 π^{2}}{2})} 。 \end{array}$ (10)

(3)广义S变换。通过引入与频率相关的可变因子σ _f, 可以得到一种新的广义S变换^{[33, 34, 35]}, 用于处理时间序列, 将时间域信号转换为频率域数据, 公式为

$g_{f} (t) = \frac{|f|}{σ_{f} \sqrt[]{2 π}} e^{- \frac{t^{2} f^{2}}{2 σ_{f}^{2}}} 。$ (11)

式中: σ _f是一个以频率f为自变量的函数因子, 可根据不同的需要定义不同类型的函数。

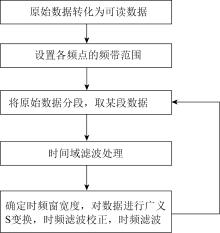
基于广义S变换的大地电磁场时间序列处理流程如图(3)所示, 通过广义S变换得到电磁场时频谱。

	Figure Option View Download New Window
	图3 基于广义S变换的时间序列处理流程Fig.3 Time series processing flow based on generalized S-transform

2.2.2 数据去噪处理

数据去噪包含时间域去噪和频率域去噪两类方式。

(1)独立分量分析。独立分量分析算法是一种时间序列处理方法, 将n个源信号的独立分量分析转换为对n个优化问题的求解, 即将混合的信号逐个分离。该方法的线性模型^[36]可以表示为

$x = As = \overset{n}{\sum_{i}} a_{i} s_{i}, i = 1, 2, \dots, n 。$ (12)

式中: s_i为独立分量; A=(a₁, a₂, …, a_n)∈ Rⁿ^×ⁿ为混合满秩矩阵; a_i是混合矩阵的基向量。当进行独立分量分析时, 数据首先要进行白化处理, 单向量的有如下表达形式

$\begin{array}{l} ω (i) = E {xg (ω^{T} (i - 1) x)} - E {g' (ω^{T} (i - \\ 1) x)} ω (i - 1) 。 \end{array}$ (13)

式中: ω 为权向量。利用迭代方法调整权向量, 直至算法收敛, 获得新的独立分量y₁= ${\hat{s}}_{1}$ =ω x, 实现时间序列信噪分离。

(2)远参考去噪。当本地信号存在噪声时, 传递函数中的自功率谱项会放大信号噪声。在一定区域范围内, 以往研究显示测点与远参考点的磁场分量信号相关, 而噪声不相关, 于是提出远参考数据处理技术^{[27, 37]}, 用以削弱或消除磁场不相关噪声。该技术要求在远区(50~100 km外)布置一个“ 安静” (背景噪声较弱)的辅助测点。此外, 由于参考点和实测测点电场变化强烈, 因此主要采用磁场参考方式, 通过测点阻抗张量和远参考磁场(H_r)卷积实现去噪, 公式为

$\begin{array}{l} Z = (H_{r}^{†} {H)}^{- 1} (H_{r}^{†} E), \\ < E_{x} H_{xr}^{*} > = Z_{xx} < H_{x} H_{xr}^{*} > + Z_{xy} < H_{y} H_{xr}^{*} >, \\ < E_{x} H_{yr}^{*} > = Z_{xx} < H_{x} H_{yr}^{*} > + Z_{xy} < H_{y} H_{yr}^{*} >, \\ < E_{y} H_{xr}^{*} > = Z_{yx} < H_{x} H_{xr}^{*} > + Z_{yy} < H_{y} H_{xr}^{*} >, \\ < E_{y} H_{yr}^{*} > = Z_{yx} < H_{x} H_{yr}^{*} > + Z_{yy} < H_{y} H_{yr}^{*} > 。 \end{array}$ (14)

式中: * 为卷积; † 为复共轭转置。

随后, 基于远参考方法提出多参考阵列数据去噪方法^{[37, 38, 39]}, 将多个参考道数据视为阵列矢量, 通过稳健主成分分析估计可靠阻抗张量。

(3)信噪分离去噪。作为一种频率域方法, 信噪分离方法利用弱噪声的远参考磁场数据H_r, 估算测点分离张量, 分离测点磁场数据H中的有效信号H_MT和噪声H_CN, 并估算测点阻抗张量和相关噪声的传递函数^[32]

$H = H_{r} T + H_{CN} 。$ (15)

倾子T为分离张量

$T = (H_{r}^{T} ω H_{r})^{- 1} (H_{r}^{T} ωH) 。$ (16)

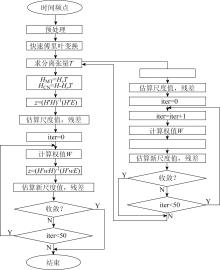
依据式(14), 利用远参考数据能够获得信噪分离后的阻抗张量, 具体流程如图4所示。

	Figure Option View Download New Window
	图4 信噪分离方法流程Fig.4 Flow of signal-noise separation method

(4)形态滤波去噪。形态滤波法^[30]假设经采样得到的待处理一维信号为f(n)(n为元素编号), 定义域为F={0, 1, …, N-1}; 结构元素为g(m), 定义域为G={0, 1, …, M-1}。采用相同的结构元素, 通过不同顺序将开运算和闭运算进行级联组合, 构建一类形态开-闭和形态闭-开滤波器, 分别定义如下

$[(f) OC (g)] (n) = (f \cdot g \cdot g) (n),$ (17)

$\begin{array}{l} [(f_{0}) CO (g_{0})] (n) = (f_{0} \cdot g_{0} \cdot g_{0}) (n) 。 \end{array}$ (18)

式中: OC表示形态开-闭滤波器; CO表示形态闭-开滤波器; · 表示开运算; · 表示闭运算。

为了有效滤除各种噪声干扰, 常采用形态开-闭和形态闭-开的平均组合形态滤波器, 用于信号的非线性滤波输出, 公式为

$y (n) = \frac{1}{2} {[(f) OC (g)] + [(f) CO (g)]} 。$ (19)

式中: y(n)表示平均组合形态滤波器的输出结果。

当信号的先验信息可以确定时, 滤波效果不仅取决于运算方式的组合, 还取决于结构元素的选取。信号中实际被滤除的成分由结构元素确定。常见的结构元素类型有矩形、直线、圆盘、三角形、抛物线(图5)。

	Figure Option View Download New Window
	图5 常见结构元素类型示意图^[29]Fig.5 Schematic diagram of common structural element types^[29]

通过参数k和L的调整改变圆盘、三角形、矩形和抛物线结构元素的幅度和宽度, 从而控制结构元素的尺度。

实验结果证明, 圆盘结构元素能够有效压制白噪声, 三角形结构元素能够有效压制脉冲噪声。然而, 实测噪声往往是多类噪声的叠加, 采用单一的结构元素难以取得较好的滤波效果。当测点中所受的噪声干扰类型比较单一时, 形态滤波具有较好的噪声抑制能力^[30]。

2.2.3 传递函数计算

传递函数, 即阻抗张量、倾子矢量、视电阻率和相位等参数, 其计算主要采用统计方式。

(1)阻抗张量最小二乘估计。阻抗张量最小二乘估计法的基本原理是双变量的线性回归理论, 表示为

$\begin{array}{l} E_{x} (ω) A = Z_{xx} (ω) H_{x} (ω) A + Z_{xy} H_{y} (ω) A, \\ E_{y} (ω) A = Z_{yx} (ω) H_{x} (ω) A + Z_{yy} H_{y} (ω) A 。 \end{array}$ （20）

式中: A和B分别可取 $E_{x}^{*}$ (ω ), $E_{y}^{*}$ (ω ), $H_{x}^{*}$ (ω )及 $H_{y}^{*}$ (ω )。阻抗张量Z_ij(i=x, y)公式为

$\begin{array}{l} Z_{xx} = \frac{< E_{x} A > < H_{y} B > - < E_{x} B > < H_{y} A >}{< H_{x} A > < H_{y} B > - < H_{x} B > < H_{y} A >}, \\ Z_{xy} = \frac{< E_{x} A > < H_{x} B > - < E_{x} B > < H_{x} A >}{< H_{y} A > < H_{x} B > - < H_{y} B > < H_{x} A >}, \\ Z_{yx} = \frac{< E_{y} A > < H_{y} B > - < E_{y} B > < H_{y} A >}{< H_{x} A > < H_{y} B > - < H_{x} B > < H_{y} A >}, \\ Z_{yy} = \frac{< E_{y} A > < H_{x} B > - < E_{y} B > < H_{x} A >}{< H_{y} A > < H_{x} B > - < H_{y} B > < H_{x} A >} 。 \end{array}$ （21）

式中: A、B分别可取 $E_{x}^{*}$ (ω )、 $E_{y}^{*}$ (ω )、 $H_{x}^{*}$ (ω )及 $H_{y}^{*}$ (ω ), 但 $E_{x}^{*}$ (ω )和 $H_{y}^{*}$ (ω )、 $E_{y}^{*}$ (ω )和 $H_{x}^{*}$ (ω )组合不可用, 实际可行的算法只有4种。

与阻抗张量的估算方法类似, 基于倾子矢量式(5)得到倾子矢量T计算方程

$\begin{array}{l} T_{x} = \frac{< H_{z} H_{x}^{*} > < H_{y} H_{y}^{*} > - < H_{z} H_{y}^{*} > < H_{y} H_{x}^{*} >}{< H_{x} H_{x}^{*} > < H_{y} H_{y}^{*} > - < H_{x} H_{y}^{*} > < H_{y} H_{x}^{*} >}, \\ T_{y} = \frac{< H_{z} H_{y}^{*} > < H_{x} H_{x}^{*} > - < H_{z} H_{x}^{*} > < H_{x} H_{y}^{*} >}{< H_{x} H_{x}^{*} > < H_{y} H_{y}^{*} > - < H_{x} H_{y}^{*} > < H_{y} H_{x}^{*} >} 。 \end{array}$ （22）

(2)阻抗张量的Robust方法。Robust方法以传递函数最小二乘估计结果为初始模型, 根据观测值与预测值误差设置权函数, 更新传递函数, 不断迭代, 直至传递函数达到精度要求。该方法的重点在于权函数的选择^[40], 不同的权函数代表着不同的Robust方法。

Huber^[40]定义的权函数(ω _ii)为

$\{\begin{array}{l} ω_{ii} = 1 & | x_{i} | \leq a \\ ω_{ii} = \frac{a}{| x_{i} |} & | x_{i} | > a \end{array} 。$ （23）

式中: x_i表示数据的残差, 初始值为|x_i|=a, Z=(H^†ω H)^-1(H^†ω E); a为阈值。

2.3 大地电磁测深数据分析

目前普遍应用的测深数据处理解释流程中, 大地电磁测深数据经处理获得阻抗张量和倾子矢量后, 一般不直接开展地下电性结构反演建模, 而是先利用数据分析方法定性认识地下介质维性和电性主轴方向, 用以确定适合的反演维度和方法。分析方法主要针对阻抗张量(电磁场)和倾子矢量(纯磁场)两类数据, 其中基于阻抗张量数据分析发展出了相位张量分析方法。

2.3.1 数据旋转

通过阻抗张量旋转^[41], 寻找阻抗张量反对角元素的最大角度或主对角元素的最小角度, 定义为电性主轴方向, 代表构造走向。需要注意的是, 电性主轴方向具有90° 的不确定性, 需依据先验信息确定可靠构造走向, 阻抗张量公式表示为

$Z_{r} = [\begin{array}{l} \cos θ & \sin θ \\ - \sin θ & \cos θ \end{array}] [\begin{array}{l} Z_{xx} & Z_{xy} \\ Z_{yx} & Z_{yy} \end{array}] [\begin{array}{l} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}] 。$ （24）

式中: Z_r为旋转后的阻抗张量; θ 为旋转角度; 当Z_xx和Z_yy趋近于0时, θ 和θ +90° 为电性主轴方向。

2.3.2 二维偏离度计算

Swift^[41]定义了阻抗张量二维偏离度, 表示为

$S = |\frac{Z_{xx} + Z_{yy}}{Z_{xy} - Z_{yx}}| 。$ (25)

二维偏离度S是一个旋转不变量, 值越小表明地下介质更趋近二维分布, 值越大代表地下介质更接近三维结构。然而, 当测深数据存在因局部3D异常体引起的数据畸变时(静位移效应), 二维偏离度因阻抗张量分解包含静位移因素而不能得到可靠结果。

利用倾子矢量也可以定义一个类似参数, 即倾子矢量二维偏离度, 表示为^[42]

$S = \frac{2 (T_{xr} T_{yi} - T_{xi} T_{yr})}{| T_{x} |^{2} + | T_{y} |^{2}} 。$ (26)

式中: r表示倾子元素实部; i表示虚部。

2.3.3 Bahr数据分析

当电磁场信号的趋肤深度达到浅表不均匀体规模的几倍时, 产生“ 非感应” 响应(电流效应)。通常, 这种受电流畸变影响的大地电磁测深数据可以被描述为一个叠加或者分解模型^[20], 即观测数据可以分为两部分: ①地下介质引起的感应响应; ②由不均匀体引起的畸变效应。此时, 阻抗张量及电性主轴需考虑“ 非感应” 响应。根据畸变影响的特点, “ 非感应” 响应通常可用畸变矩阵描述

$\begin{array}{l} \begin{array}{l} S_{1} = Z_{xx} + Z_{yy} & S_{2} = Z_{xy} + Z_{yx} \\ D_{1} = Z_{xx} - Z_{yy} & D_{2} = Z_{xy} - Z_{yx} \end{array}\}, \\ A = [S_{1}, D_{1}] + [S_{2}, D_{2}], \\ B = [S_{1}, S_{2}] - [D_{1}, D_{2}] 。 \end{array}$ (27)

式中: 运算符[ ]表示求取两个复数元素的相位差([x, y]=x_ry_i-y_rx_i, r为实部, i为虚部)。以往研究结果认为阻抗张量幅值受“ 非感应” 响应影响, 而相位不受影响。但实际情况有所不同, 基于此Bahr^[43]提出一种基于相位数据的分析方法, 假设数据旋转至电性主轴方向时, 阻抗张量同一列的元素具有相同的相位, 因此得到电性主轴方向θ ^{[20, 43]}

$\tan θ = \pm \sqrt[]{1 + {(\frac{A}{B})}^{2}} - \frac{A}{B} 或 \tan (2 θ) = \frac{B}{A} 。$ (28)

此外, Bahr提出基于相位信息的二维偏离度η

$η = \frac{(| [D_{1}, S_{2}] | - [S_{1}, D_{2} {])}^{1 / 2}}{D_{2}} 。$ (29)

2.3.4 阻抗张量分解

以往研究结果认为阻抗相位不受局部电场畸变影响, Bahr^[43]首先提出基于相位信息的区域电性主轴分析方法。而由积累电荷引起的畸变效应可用一个元素为实数的畸变矩阵表示, 该矩阵不依赖于频率, 而Groom等^[44]提出的GB分解方法解决了2D/3D结构背景下MT阻抗张量的畸变校正以及主轴方向估计问题, GB分解方法也是应用最为广泛的方法。在GB分解方法中, 阻抗张量表示为旋转矩阵、二维阻抗张量(|Z_xx|和|Z_yy|极小)及畸变矩阵综合方程^[44]

$\begin{array}{l} Z_{n} = RC Z_{2 D} R^{T}, \\ C = gTSA 。 \end{array}$ (30)

式中: Z_n为阻抗张量观测值; R为旋转矩阵, 其元素为关于电性主轴角的三角函数值; Z₂_D为2D电性结构条件下的区域阻抗张量(Z_xx=0, Z_yy=0); C为由电场引起的畸变矩阵(元素为实数), 可分解为扭曲角矩阵T, 剪切角矩阵S, 各向异性因子矩阵A及静位移因子常数g的乘积。这里, GB分解方程是欠定问题, 只有8个已知参数(4个复数形式的阻抗张量Z), 但有9个未知参数(电性主轴角度θ , 4个实数形式的畸变矩阵C, 2个复数形式的区域阻抗张量元素Z₂_D)。而且, 以往基于一维和二维电磁场理论假设的研究结果对静位移效应的认识和数学表达不准确^[45], 因此, 这里不考虑静位移效应。此外, 不考虑未知数更多的各向异性张量, 使GB分解方程未知数降为7个, 经简化后方程为

$\begin{array}{l} Z = [\begin{array}{l} Z_{xx} & Z_{xy} \\ Z_{yx} & Z_{yy} \end{array}] = RTS Z_{2 D} R^{T} = [\begin{array}{l} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}], \\ [\begin{array}{l} 1 - te & e - t \\ e + t & 1 + te \end{array}] [\begin{array}{l} 0 & a \\ b & 0 \end{array}] [\begin{array}{l} \cos θ & \sin θ \\ - \sin θ & \cos θ \end{array}] 。 \end{array}$ (31)

式中: θ 为区域2D电性主轴角度, 其三角函数构成旋转矩阵; t, e分别为扭曲角和剪切角; a, b分别为区域电性主轴坐标系上阻抗张量矩阵的两个反对角线元素。对于传统的GB分解方程, 可通过共轭梯度等最优化方法进行求解, 其中θ 是目前应用较为广泛的参数。

2.3.5 含各向异性信息的GB分解

GB分解也是针对阻抗张量的一种数据分析方法, 传统的GB分解方法, 将静位移因子常数g及各向异性矩阵A并入区域阻抗张量中, 忽略了地下介质电阻率各向异性的影响。谢成良^[42]将常数项g融入2D区域阻抗张量, 保留各向异性参数, 表示为

$\begin{array}{l} Z_{m} = [\begin{array}{l} Z_{xx} & Z_{xy} \\ Z_{yx} & Z_{yy} \end{array}] = RTSA Z_{2 D} R^{T} = [\begin{array}{l} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}] \\ [\begin{array}{l} 1 - te & e - t \\ e + t & 1 + te \end{array}] [\begin{array}{l} 1 + s & 0 \\ 0 & 1 - s \end{array}] [\begin{array}{l} 0 & a \\ - b & 0 \end{array}] \\ [\begin{array}{l} \cos θ & \sin θ \\ - \sin θ & \cos θ \end{array}] 。 \end{array}$ (32)

与传统GB分解方法相比, 新方法在计算效率、稳定性等方面有一定优势。

2.3.6 相位张量分析

Caldwell等^[46]提出相位张量, 并基于3个旋转不变量和一个非旋转不变量提出数据分析方法。相位张量ϕ 表示为

$ϕ = [\begin{array}{l} ϕ_{11} & ϕ_{12} \\ ϕ_{21} & ϕ_{22} \end{array}] = Z_{r}^{- 1} Z_{i} 。$ (33)

相位张量不受电流畸变影响, 能够得到α 、β 、II₁和II₂四个参数

$\begin{array}{l} \tan 2 α = \frac{ϕ_{12} + ϕ_{21}}{ϕ_{11} - ϕ_{22}}, \\ \tan 2 β = \frac{ϕ_{12} - ϕ_{21}}{ϕ_{11} + ϕ_{22}}, \\ I I_{1} = \frac{1}{2} [(ϕ_{11} - ϕ_{22})^{2} + (ϕ_{12} + ϕ_{21})^{2}]^{1 / 2}, \\ I I_{2} = \frac{1}{2} [(ϕ_{11} + ϕ_{22})^{2} + (ϕ_{12} - ϕ_{21})^{2}]^{1 / 2} 。 \end{array}$ (34)

相位张量椭圆函数α 是主轴方位角, 可以判断研究区域构造走向, 长半轴ϕ _max=II₁+II₂、短半轴ϕ _min=II₂-II₁对应相互垂直的电流移动方向(电性主轴方向, 但有90° 的不确定度); 填充颜色为β (偏离角), 其绝对值与介质维度正相关(曲率|β |数值较小时, 指示一维或二维介质; |β |较大时指示三维介质)。

根据参数β 及II₁的取值, 也可以判断介质维度^[47]: ①地下一维介质: β 及II₁均为零; ②地下二维介质, β 为零, II₁非零; ③地下三维介质, β 非零。

2.3.7 感应矢量/倾子分析

利用倾子计算得到的感应矢量I能够用于分析介质维性和区域主轴方向, 但其稳定性不高, 表达式为^[48]

$I = T_{x} - T_{y} 。$ (35)

式中: I为感应矢量, T_x和T_y是倾子的两个分量。以往研究结果显示实感应矢量的方向指向低阻体、背离高阻体, 矢量的幅值表征了介质横向不均匀性程度(幅值大表示横向不均匀性强, 幅值小则表示横向不均匀性较弱)。根据这一特点, 可以大致圈定地下导电异常体的范围。一维结构条件下, 实感应矢量和虚感应矢量均为0; 二维结构的实感应矢量和虚感应矢量的方向相互平行; 三维结构的实感应矢量和虚感应矢量的方向相互垂直。

3 总结与展望

本文针对大地电磁测深方法的基本原理及其数据处理与分析方法, 介绍了前人研究成果。其中数据处理方法包括快速傅里叶变换、小波变换、广义S变换、独立分量分析、远参考去噪、信噪分离去噪、形态滤波去噪、阻抗的最小二乘估计、阻抗的Robust估计等方法。数据分析方法包括数据旋转、二维偏离度计算、Bahr数据分析、阻抗张量分解、含各向异性信息的GB分解、相位张量分析、感应矢量/倾子分析等方法。

上述方法各有优缺点, 需针对不同的实际情况选用不同方法。高信噪比、高质量数据条件下, 不同数据处理和分析方法的结果和结论具有较强的一致性。然而, 对于噪声强干扰数据和地形、不均匀体引起的畸变数据, 不同的方法其结果略有出入, 需要依据噪音和畸变类型选择有效方法进行数据处理和分析。例如: 数据处理中Robust估计能够消除瞬时强噪音干扰, 但不能消除长时间噪音干扰; 远参考方法能够消除不相关噪声干扰, 但对相关噪声较为乏力。数据分析中普遍认为倾子矢量对高导介质更为敏感和准确, 但极易受噪音干扰; 阻抗张量分析结果更为精确, 但较相位张量更容易受到电场畸变影响。目前, 较为普适的数据处理分析流程为快速傅里叶变换— 远参考处理— 传递函数计算— 功率谱编辑— 数据筛选— 阻抗张量分析— 相位张量分析。

未来, 随着数学方法和计算技术的不断进步, 有望研发出基于普适性更强或者依据数据自动选择技术路线的新的指导型处理解释方法, 适用于各种地质、噪声环境并获得最佳处理结果。

(责任编辑: 王晗)

参考文献

文献选项

[1]	Tikhonov A. The determination of electrical properties of deep la-yer of the Earth's crust[J]. Doklady Akademii Nauk Sssr, 1950, 73: 295-297. [本文引用:1]
[2]	Cagniard L. Basic theory of the magneto-telluric method of geophysical prospecting[J]. Geophysics, 1953, 18(3): 605-635. [本文引用:2]
[3]	吕庆田, 吴明安, 汤井田等. 安徽庐枞矿集区三维探测与深部成矿预测[M]. 北京: 科学出版社, 2018. Lv Q T, Wu M G, Tang J T, et al. Three-dimensional Detection and Deep Mineralization Prediction of Lucong Ore Cluster in Anhui Province[M]. Beijing: Science Press, 2018. [本文引用:1]
[4]	Zhang K, Lv Q T, Zhao J H, et al. Magnetotelluric evidence for the multi-microcontinental composition of eastern South China and its tectonic evolution[J]. Scientific Reports, 2020, 10(1): 13105. [本文引用:1]
[5]	Zhang K, Lv Q T, Yan J Y, et al. The three-dimensional electrical structure and metallogenic prospect of the Ning (Nanjing)-Wu (Wuhu) basin and the southern adjacent area in eastern China[J]. Journal of Asian Earth Sciences, 2019, 173: 304-313. [本文引用:2]
[6]	Zhang K, Lv Q, Zhao J, et al. Intra-continental Orogeny: Insights from Magnetotelluric Data into the Mesozoic Uplift History of the Eastern Jiangnan Orogen in South China[J]. Acta Geologica Sinica-English Edition, 2023, 97(1): 55-67. [本文引用:1]
[7]	Zhang Kun, Lv Q T, Yan J Y, et al. The electrical resistivity signature of a fault controlling gold mineralization and the implications for Mesozoic mineralization: A case study from the Jiaojia Fault, eastern China[J]. Acta Geophysica; 2017a, 65(2): 1-15. [本文引用:1]
[8]	Zhang Kun, Lv Q T, Yan J Y, et al. Crustal structure beneath the Jiaodong Peninsula, North China, revealed with a 3D inversion model of magnetotelluric data[J]. Journal of Geophysics & Engineering; 2018, 15 2442-245. [本文引用:1]
[9]	赵凌强, 孙翔宇, 詹艳, 等. 银川盆地三维深部电性结构特征及其地球动力学意义[J]. 中国科学: 地球科学, 2023, 53(3): 481-496. Zhao L Q, Sun X Y, Zhan Y, et al. Three-dimensional deep electrical structure characteristics of Yinchuan Basin and its geodynamic significance[J]. Science China: Earth Sciences, 2023, 53(3): 481-496. [本文引用:1]
[10]	薛国强, 陈卫营, 赵平, 等. 西藏羊八井地热田三维电性结构模型——来自大地电磁的证据[J]. 中国科学: 地球科学, 2023, 53(08): 1859-1871. Xue G Q, Chen W Y, Zhao P, et al. Three-dimensional electrical structure model of Yangbajing geothermal field in Tibet: Evidence from magnetotellurics[J]. Science China: Earth Sciences, 2023, 53(08): 1859-1871 [本文引用:2]
[11]	张昆. 华南地区大地电磁应用示范[Z]. 北京: 地质调查项目进展报告, 2023. Zhang K. Demonstration of magnetotelluric applications in South China[Z]. Beijing: Geological Survey Project Progress Report, 2023. [本文引用:1]
[12]	张昆. 改进的大地电磁场非线性共轭梯度三维反演及其并行计算研究[D]. 北京: 中国地质大学(北京), 2013. Zhang K. Research on Improved Three-dimensional Inversion of Nonlinear Conjugate Gradient of Magnetotelluric Field and Its Parallel Computing[D]. Beijing: China University of Geosciences (Beijing), 2013. [本文引用:1]
[13]	陈乐寿, 王光锷. 大地电磁测深法[M]. 北京: 地质出版社, 1990. Chen L S, Wang G E. Magnetotelluric Sounding Method[M]. Beijing: Geological Publishing House, 1990. [本文引用:4]
[14]	Zhang K, Wei W B, Lv Q T. Four changes for efficiency and practicality on previous 3D MT NLCG inversion algorithm[J] Acta Geod Geophys, 2014, 49: 551-563. [本文引用:1]
[15]	Zhang K, Yan J Y, Lv Q T, et al. Three-dimensional nonlinear conjugate gradient parallel inversion with full information of marine magnetotellurics[J]. Journal of Applied Geophysics, 2017b, 139: 144-157. [本文引用:1]
[16]	崔金岭. 强干扰地区电磁噪声与大地电磁测深数据处理新方法研究[D]. 北京: 中国地质大学(北京), 2014. Cui J L. Research on New Methods of Electromagnetic Noise and Magnetotelluric Sounding Data Processing in Strong Interference Areas[D]. Beijing: China University of Geosciences (Beijing), 2014. [本文引用:2]
[17]	林昌洪, 谭捍东, 佟拓. 倾子资料三维共轭梯度反演研究[J]. 地球物理学报, 2011. , 54(4): 1106-1113. Lin C H, Tan H D, Tong T. Study on three-dimensional conjugate gradient inversion of dipole data[J]. Chinese Journal of Geophysics, 2011. ,54(4): 1106-1113. [本文引用:1]
[18]	自然资源部. DZ/T 0173—2022大地电磁测深法技术规程大地电磁测深法技术规程[S]. 北京: 地质出版社, 2022. Ministry of Natural Resources. DZ/T 0173—2022 Technical Specifications for Magnetotelluric Sounding Technical Specifications for Magnetotelluric Sounding[S]. Beijing: Geological Publishing House, 2022. [本文引用:1]
[19]	石应骏, 刘国栋, 吴广耀, 等. 大地电磁测深法教程[M]. 北京: 地质出版社, 1985. Shi Y J, Liu G D, Wu G Y, et al. Tutorial on Magnetotelluric Sounding[M]. Beijing: Geological Publishing House, 1985. [本文引用:1]
[20]	Fiona S, Karsten B. Practical magnetotellurics[M]. Cambridge University Press, 2005. [本文引用:3]
[21]	Parzen E. Mathematical Considerations in the Estimation of Spectra[J]. Technometrics, 1961, 3(2): 167-190. [本文引用:1]
[22]	Parzen E. Modern Probability Theory and Its Applications[M]. online: John Wiley & Sons, 1992. [本文引用:1]
[23]	Jenkins G W, Watts DG. Spectral Analysis and its Applications[J]. San Francisco: Holden-Day, 1968. [本文引用:1]
[24]	Egbert G D, Booker JR. Robust estimation of geomagnetic transfer functions[J]. Geophysical Journal International, 1986, 87(1): 173-194. [本文引用:2]
[25]	Mebane W, Sekhon J. Robust estimation and outlier detection for overdispersed multinomial models of count data[J]. American Journal of Political Science, 2004, 48(2): 392-411. [本文引用:1]
[26]	Jones A G, Chave AD, Egbert G, et al. A comparison of techniques for magnetotelluric response function estimation[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B10): 14201-14213. [本文引用:2]
[27]	Gamble T D, Goubau WM, Clarke J. Magnetotellurics with a remote magnetic reference[J]. Geophysics, 1979, 44(1): 53-68. [本文引用:2]
[28]	徐义贤, 王家映. 基于连续小波变换的大地电磁信号谱估计方法[J]. 地球物理学报, 2000, 43(5): 677-683. Xu Y X, Wang J Y. Spectrum estimation method of magnetotelluric signals based on continuous wavelet transform[J]. Chinese Journal of Geophysics, 2000, 43(5): 677-683. [本文引用:1]
[29]	Garcia X, Jones A G. Robust processing of magnetotelluric data in the AMT dead band using the continuous wavelet transform[J]. Geophysics, 2008, 73(6): F223-F234. [本文引用:1]
[30]	汤井田, 李晋, 肖晓, 等. 数学形态滤波与大地电磁噪声压制[J]. 地球物理学报, 2012, 55(5): 1784-1793. Tang J T, Li J, Xiao X, et al. Mathematical morphology filtering and magnetotelluric noise suppression[J]. Chinese Journal of Geophysics, 2012, 55(5): 1784-1793. [本文引用:3]
[31]	Egbert G D. Robust multiple-station magnetotelluric data processing[J]. Geophysical Journal International, 1997, 130(2): 475-496. [本文引用:1]
[32]	Larsen J C, Mackie R L, Manzella A, et al. Robust smooth magnetotelluric transfer functions[J]. Geophysical Journal International, 1996, 124(3): 801-819. [本文引用:2]
[33]	Wang L, Meng X F. An adaptive Generalized S-transform for instantaneous frequency estimation[J]. Signal Processing, 2011, 91(8): 1876-1886. [本文引用:1]
[34]	周竹生, 陈友良. 含可变因子的广义S变换及其时频滤波[J]. 煤田地质与勘探, 2011, 39(6): 63-66. Zhou Z S, Chen Y L. Generalized S transform with variable factors and its time-frequency filtering[J]. Coal Geology and Exploration, 2011, 39(6): 63-66. [本文引用:1]
[35]	Liu J, Yao J, Liu X. Generalized S transform with adaptive optimized window and its application in seismic signal analysis[J]. Information Technology Journal, 2013, 12(2): 276. [本文引用:1]
[36]	Back A D, Weigend A S. A first application of independent component analysis to extracting structure from stock returns[J]. International journal of neural systems, 1997, 8(04): 473-484. [本文引用:1]
[37]	Chave A D, Thomson D J. Bounded influence magnetotelluric response function estimation[J]. Geophysical Journal International, 2004, 157(3): 988-1006. [本文引用:2]
[38]	Egbert G D. Processing and interpretation of electromagnetic induction array data[J]. Surveys in geophysics, 2002, 23(2/3): 207-249. [本文引用:1]
[39]	周聪, 汤井田, 原源, 等. 强干扰区含噪电磁场的时空分布特征[J]. 吉林大学学报: 地球科学版, 2020, 50(6): 17. Zhou C, Tang J T, Yuan Y, et al. Temporal and spatial distribution characteristics of noisy electromagnetic fields in strong interference areas[J]. Journal of Jilin University: Earth Science Edition, 2020, 50(6): 17. [本文引用:1]
[40]	Huber P J. Robust Statistics[M]. New York: Wiley, 1981. [本文引用:2]
[41]	Swift C M. A Magnetotelluric Investigation of An Electrical Conductivity Anomaly in the Southwestern United States[D]. Massachusetts Institute of Technology, 1967. [本文引用:2]
[42]	谢成良. 大地电磁测深资料综合处理软件系统研究[D]. 北京: 中国地质大学 (北京), 2013 Xie C L. Research on Software System for Comprehensive Processing of Magnetotelluric Sounding Data[D]. Beijing: China University of Geosciences (Beijing), 2013. [本文引用:2]
[43]	Bahr K. Interpretation of the magnetotelluric impedance tensor: regional induction and local telluric distortion[J]. Journal of geophysics, 1988, 62(1): 119-127. [本文引用:3]
[44]	Groom R W, Bailey R C. Decomposition of magnetotelluric impedance tensors in the presence of local three-dimensional galvanic distortion[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B2): 1913-1925. [本文引用:2]
[45]	Zhang K, Wei W, Lu Q, et al. Correction of magnetotelluric static shift by analysis of 3D forward modelling and measured test data[J]. Exploration Geophysics, 2016, 47. [本文引用:1]
[46]	Caldwell T G, Bibby H M, Brown C. The magnetotelluric phase tensor[J]. Geophysical Journal International, 2004, 158(2): 457-469. [本文引用:1]
[47]	Bibby H, Caldwell T, Brown C. Determinable and non-determinable parameters of galvanic distortion in magnetotellurics[J]. Geophysical Journal International, 2005, 163(3): 915-930. [本文引用:1]
[48]	Parkinson W D. The influence of continents and oceans on geomagnetic variations. Geophysical Journal International[J]. Geophysical Journal International, 1962, 6(4): 441-449. [本文引用:1]

1950

0.0

... 0 引言大地电磁测深(magnetotelluric sounding,MT)方法于20世纪50年代初由前苏联学者Tikhonov^[1]和法国学者Cagniard^[2]提出,该方法基于超宽频率范围(10 000~0 ...

1953

0.0

... 0 引言大地电磁测深(magnetotelluric sounding,MT)方法于20世纪50年代初由前苏联学者Tikhonov^[1]和法国学者Cagniard^[2]提出,该方法基于超宽频率范围(10 000~0 ...

... )^[2] ...

2018

0.0

... 000 1 Hz)的天然电磁场信号揭示地下不同深度尺度(地壳浅表至上百千米)的电性结构,以天然场源能量大、频带宽、勘探深度大、仪器设备轻便、不受高阻屏蔽、对低阻分辨率高等优势受到地球物理学家的关注,主要被用于矿产-地下水-地热资源勘查、油气普查、灾害调查、地壳及岩石圈深部结构研究等领域,是不可或缺的地球物理深探测方法之一^[3] ...

2020

0.0

... 其中,深部结构研究和深部找矿等领域近年来取得了一系列优秀应用成果,例如: Zhang等^[4,5,6]利用大地电磁测深剖面结果揭示了华南地区岩石圈电性结构,发现了陆内俯冲板片痕迹,并提出了对板片断裂控制成矿系统的新认识 ...

2019

0.0

... Zhang等^[5,7,8]利用大地电磁测深三维反演结果揭示胶东和长江中下游典型矿集区地壳精细结构,并提出对成矿背景和过程的新认识 ...

2023

0.0

2017a

0.0

... Zhang等^[5,7,8]利用大地电磁测深三维反演结果揭示胶东和长江中下游典型矿集区地壳精细结构,并提出对成矿背景和过程的新认识 ...

2018

0.0

... Zhang等^[5,7,8]利用大地电磁测深三维反演结果揭示胶东和长江中下游典型矿集区地壳精细结构,并提出对成矿背景和过程的新认识 ...

2023

0.0

... 赵凌强等^[9]使用5条完全覆盖贺兰山#cod#x02014 ...

2023

0.0

... 薛国强等^[10]利用测大地电磁全阻抗张量数据给出了羊八井地热田三维电性结构模型在不同深度的水平切片和在不同测线的剖面图,发现羊八井地热田的深部热源 ...

... 数据分析主要包括电性主轴方向、介质维度分析、极化模式分析等^[10](图1) ...

2023

0.0

... 1 大地电磁测深方法基本原理大地电磁测深方法通过观测天然场源或远区人工场源的平面二分量电场以及空间三分量磁场分量信号,获得地下电阻抗和倾子信息^[11,12] ...

0.0

1990

0.0

... ₀)近似代替地下半空间介质参数^[13],而且由于电磁波的使用频率通常相对较低, 因此忽略位移电流 (-i#cod#x003c9 ...

... 根据平面波场入射理论,可以建立电阻抗(Z)与电场强度水平分量(E_x)和磁场强度水平分量(H_x)的关系表达式^[13,14,15]以及倾子矢量(T)和磁场强度(H)三分量的关系表达式^[16,17]: ...

... 2 数据处理方法MT数据处理主要指由采集的时间序列计算得到频率域的功率谱矩阵和传递函数的过程(阻抗张量、倾子矢量等)^[13,19,20],普遍应用流程为时频转换#cod#x02014 ...

... 为了消除或降低误差,一般采用最小二乘估计法获得最优统计结果^{[13,24,25,26]} ...

2014

0.0

2017b

0.0

... 而小波变换是一种时频分析方法,是一种自适应的时域和频域同时局部化方法,能够调节时频窗大小,分析低频或者高频的局部信号^[16] ...

2011

0.0

2022

0.0

... 因此,测点需远离地表障碍物、干扰源以及地形等影响^[18] ...

1985

0.0

2005

0.0

... 通常,这种受电流畸变影响的大地电磁测深数据可以被描述为一个叠加或者分解模型^[20],即观测数据可以分为两部分: ①地下介质引起的感应响应 ...

... ^[20,43] ...

1961

0.0

... 时频转换一般采用快速傅立叶变换,需要选择时窗长度、分频策略以及中心频点,得到不同时间段的功率谱矩阵,通过功率谱矩阵叠加方式获得每个频点的稳定数据^[21,22,23] ...

1992

0.0

1968

0.0

1986

0.0

... 为了消除或降低误差,一般采用最小二乘估计法获得最优统计结果^{[13,24,25,26]} ...

... Robust方法^[24]针对相关信号和不相关噪声,根据观测误差和剩余功率谱的大小对数据进行加权处理,降低强噪声干扰数据的权重,能够压制非高斯分布噪声,较最小二乘估计法有一定优势,但不能解决近场等相关噪声问题 ...

2004

0.0

... 为了消除或降低误差,一般采用最小二乘估计法获得最优统计结果^{[13,24,25,26]} ...

1989

0.0

... 为了消除或降低误差,一般采用最小二乘估计法获得最优统计结果^{[13,24,25,26]} ...

... 该方法仍然会产生一定的统计误差,并且不能消除相关噪声的影响^[26] ...

1979

0.0

... 远参考法利用远区洁净测站磁场信号数据与实测数据卷积,减弱或消除磁场不相关噪声,获得高质量阻抗张量^[27] ...

... 在一定区域范围内,以往研究显示测点与远参考点的磁场分量信号相关,而噪声不相关,于是提出远参考数据处理技术^[27,37],用以削弱或消除磁场不相关噪声 ...

2000

0.0

... 此外,前人还提出了连续小波变换^[28,29]、数学形态滤波^[30]、多参考站数据噪声统计^[31]、基于远参考磁场数据的磁场信号分离方法^[32]等,本文主要介绍数据处理的基本原理和新方法进展 ...

2008

0.0

2012

0.0

... 形态滤波法^[30]假设经采样得到的待处理一维信号为f(n)(n为元素编号), 定义域为F={0,1,…,N-1} ...

... 当测点中所受的噪声干扰类型比较单一时,形态滤波具有较好的噪声抑制能力^[30] ...

1997

0.0

1996

0.0

... 作为一种频率域方法,信噪分离方法利用弱噪声的远参考磁场数据H_r,估算测点分离张量,分离测点磁场数据H中的有效信号H_MT和噪声H_CN,并估算测点阻抗张量和相关噪声的传递函数^[32] ...

2011

0.0

... _f,可以得到一种新的广义S变换^[33,34,35],用于处理时间序列,将时间域信号转换为频率域数据,公式为 ...

2011

0.0

... _f,可以得到一种新的广义S变换^[33,34,35],用于处理时间序列,将时间域信号转换为频率域数据,公式为 ...

2013

0.0

... _f,可以得到一种新的广义S变换^[33,34,35],用于处理时间序列,将时间域信号转换为频率域数据,公式为 ...

1997

0.0

... 该方法的线性模型^[36]可以表示为 ...

2004

0.0

... 随后,基于远参考方法提出多参考阵列数据去噪方法^[37,38,39],将多个参考道数据视为阵列矢量,通过稳健主成分分析估计可靠阻抗张量 ...

2002

0.0

... 随后,基于远参考方法提出多参考阵列数据去噪方法^[37,38,39],将多个参考道数据视为阵列矢量,通过稳健主成分分析估计可靠阻抗张量 ...

2020

0.0

... 随后,基于远参考方法提出多参考阵列数据去噪方法^[37,38,39],将多个参考道数据视为阵列矢量,通过稳健主成分分析估计可靠阻抗张量 ...

1981

0.0

... 该方法的重点在于权函数的选择^[40],不同的权函数代表着不同的Robust方法 ...

... Huber^[40]定义的权函数(#cod#x003c9 ...

1967

0.0

... 通过阻抗张量旋转^[41],寻找阻抗张量反对角元素的最大角度或主对角元素的最小角度,定义为电性主轴方向,代表构造走向 ...

... Swift^[41]定义了阻抗张量二维偏离度,表示为 ...

0.0

... 利用倾子矢量也可以定义一个类似参数,即倾子矢量二维偏离度,表示为^[42] ...

... 谢成良^[42]将常数项g融入2D区域阻抗张量,保留各向异性参数,表示为 ...

1988

0.0

... 但实际情况有所不同,基于此Bahr^[43]提出一种基于相位数据的分析方法,假设数据旋转至电性主轴方向时,阻抗张量同一列的元素具有相同的相位,因此得到电性主轴方向#cod#x003b8 ...

... ^[20,43] ...

... 以往研究结果认为阻抗相位不受局部电场畸变影响,Bahr^[43]首先提出基于相位信息的区域电性主轴分析方法 ...

1989

0.0

... 而由积累电荷引起的畸变效应可用一个元素为实数的畸变矩阵表示,该矩阵不依赖于频率,而Groom等^[44]提出的GB分解方法解决了2D/3D结构背景下MT阻抗张量的畸变校正以及主轴方向估计问题,GB分解方法也是应用最为广泛的方法 ...

... 在GB分解方法中,阻抗张量表示为旋转矩阵、二维阻抗张量(|Z_xx|和|Z_yy|极小)及畸变矩阵综合方程^[44] ...

2016

0.0

... 而且,以往基于一维和二维电磁场理论假设的研究结果对静位移效应的认识和数学表达不准确^[45],因此,这里不考虑静位移效应 ...

2004

0.0

... Caldwell等^[46]提出相位张量,并基于3个旋转不变量和一个非旋转不变量提出数据分析方法 ...

2005

0.0

... 及II₁的取值,也可以判断介质维度^[47]: ①地下一维介质: #cod#x003b2 ...

1962

0.0

... 利用倾子计算得到的感应矢量I能够用于分析介质维性和区域主轴方向,但其稳定性不高,表达式为^[48] ...